Droplet Combustion Processes
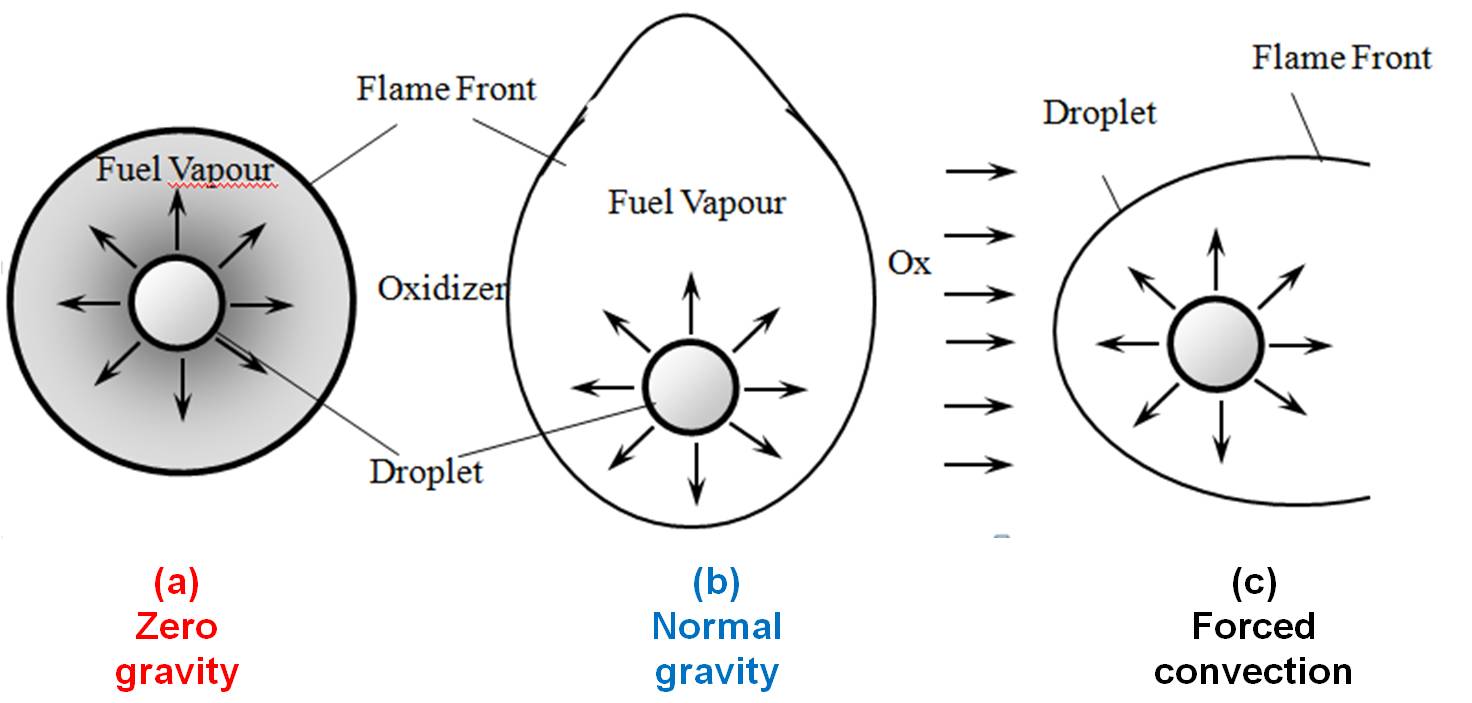
Factors affecting the shape of the flame front:
(a) Zero gravity : spherical flame front (no buoyancy)
(b) Normal gravity : elongated (due to natural convection)
(c) Forced convection condition : fame aligned with flow
Energy required to vaporize the liquid fuel (QV):

- Spherically symmetric droplet is ideal case for studying droplet combustion and describing the combustion process mathematically.
-
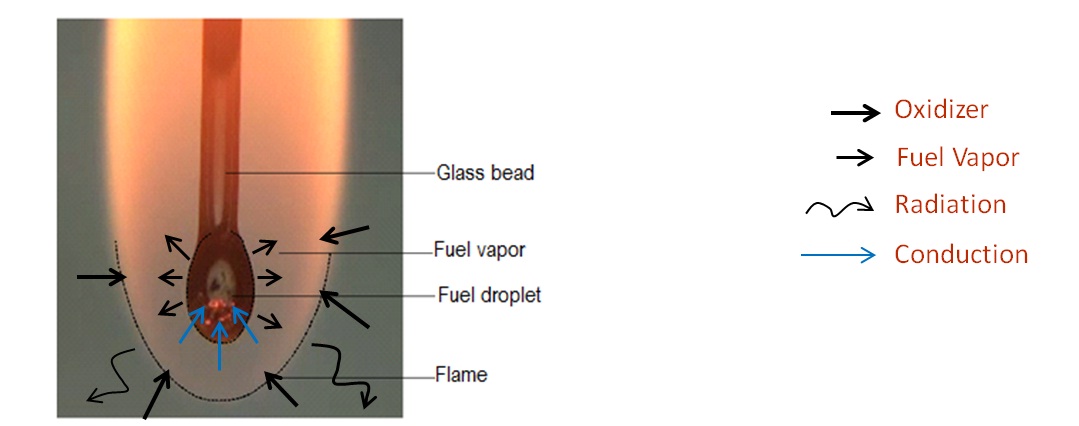
Steps in droplet combustion are (see figure for explanation):
- Fuel vaporizes at the droplet surface and diffuses outward.
- Simultaneously, oxidizer diffuses inward from the ambient environment.
- The fuel and oxidizer react stoichiometrically, resulting in a zone of intense non-premixed flame.
- Heat transfer by conduction and radiation occurs in two directions; outward from the flame to infinity and inward to the droplet surface. The inward transferred heat is utilized for liquid vaporization.
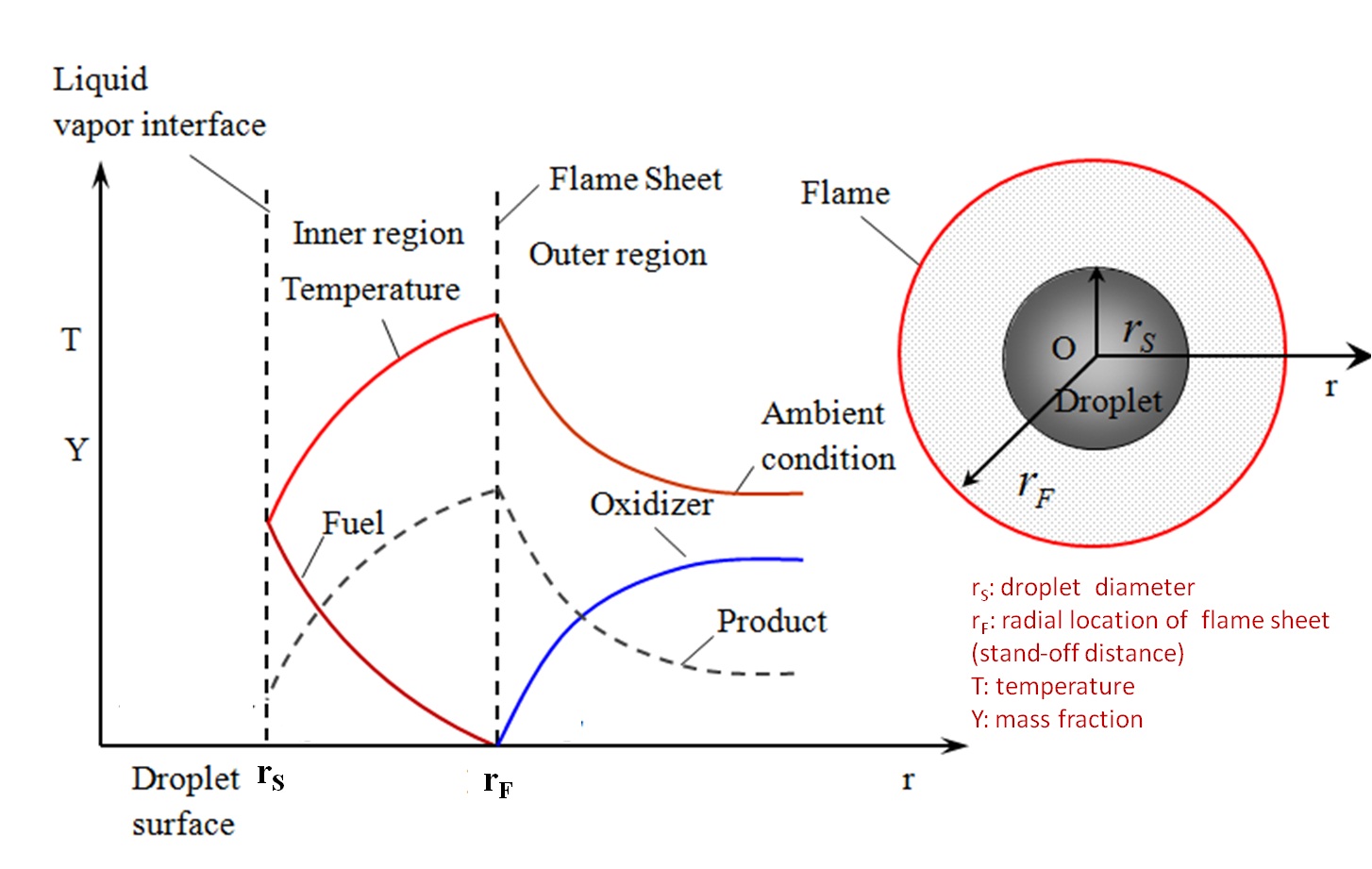
One dimensional model of droplet combustion
-
Assumptions
- Single droplet in quiescent atmosphere.
- Temperature inside the droplet is uniform.
- Density of liquid fuel much higher than the gas phase.
- Fuel is a single component with no solubility for gases.
- Flow velocities are assumed to be low.
- Single step irreversible reaction.
- Thin flame approximation is valid.
- Constant thermo-physical properties.
- Unity Lewis number.
- Radiation heat transfer is neglected.
- No other phase is formed in the liquid fuel droplet.
D2 Law
- Mathematical description is in terms of the "D2 law". The assumptions lead to closed form analytical expressions for the droplet burning rate, flame location (standoff location from the gas-liquid interface), and flame temperature.
- Refer [1] for detailed derivation.
- Brief derivation: Using continuity equation for the rate of decrease of droplet mass,
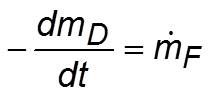
mD: mass of droplet
mF: mass burning rate of fuel
t: time
and the mass burning rate of fuel in the droplet, following expression is obtained for the rate of decrease in droplet diameter.
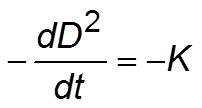
which on integration leads to the D2 law:
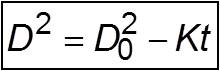
D0: initial droplet diameter
D: droplet dimeter
K: burning rate constant
- As per this model, droplet burning rate, flame stand-off location (rF), and flame temperature remain constant for the duration of droplet burning.
- We shall verify the D2 law using experimental data.