| H | = | 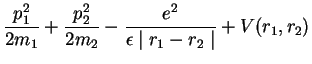 |
|
| V(r1,r2) | = | 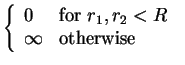 |
A simple variational approach to the ground state properties of the electron - hole system confined in a spherical well is adopted. The Hamiltonian is:
| H | = | 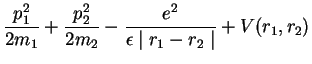 |
|
| V(r1,r2) | = | 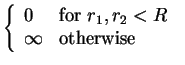 |
The subscripts refer to electron and hole. Hylleraas coordinates
are adopted and a trial wavefunction is used,
| = | 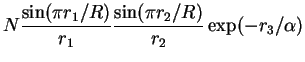 |
The degree of spatial correlation between the electron and the hole
is characterized by the variational parameter ![]() and N is the normalization constant.
and N is the normalization constant.
Kayanuma seeks to explain the optical absorption data of CuCl nanocrystallites. He supplements his calculations with interesting asymptotic analyses. In the final three paragraphs of the paper he suggest how we may estimate the size of the microcrystal by using the calculated peak energy. This work foreshadows a widely known and more extensive calculation by the same author in Phys. Rev. B 38, 9797 - 9805 (1988): ``Quantum Size Effects of Interacting Electrons and Holes in Semiconductor Microcrystals with Spherical Shape.''