| = | 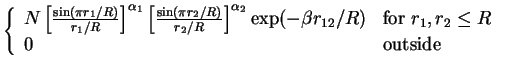 |
| = | 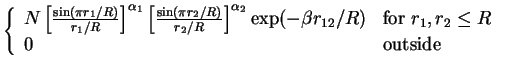 |
Here R is the radius of the spherical quantum dot (QD). The three
variational parameters are ![]() ,
,![]() and
and ![]() while
N is the normalization. The systems under study were CdS and
CuCl.
while
N is the normalization. The systems under study were CdS and
CuCl.
The authors consider the case of weak confinement (e.g. size R
>
aB, the bulk exciton radius). One would expect, from
the work of Efros & Efros (1982), the energy upshift ![]() to go as
to go as
| = | 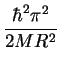 |
where
| M | = | m1 + m2 |
The authors try to extract M from the slope of ![]() vs. 1 /
R2 but are unsuccessful. This failure led them
to suggest that the QD must be modeled by a finite and not infinite
potential depth. The authors also plot the oscillator strength as a function
of
aB* / R using the Henry and Nassau
formula. This reveals a sharp rise as R is reduced. Over the years Prof.
Rustagi's group has produced a series of papers employing both effective
mass theory (EMT) and tight-binding (TB) methods.
vs. 1 /
R2 but are unsuccessful. This failure led them
to suggest that the QD must be modeled by a finite and not infinite
potential depth. The authors also plot the oscillator strength as a function
of
aB* / R using the Henry and Nassau
formula. This reveals a sharp rise as R is reduced. Over the years Prof.
Rustagi's group has produced a series of papers employing both effective
mass theory (EMT) and tight-binding (TB) methods.