Theorem 7.1.1. [Generalized Schur’s Theorem] Let A ∈ Mn(ℂ). Suppose λ1,…,λk are the distinct eigenvalues of A with multiplicities m1,…,mk, respectively. Then, there exists a non-singular matrix W such that
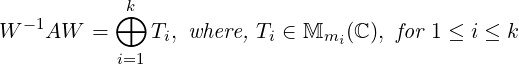
We start this chapter with the following theorem which generalizes the Schur Upper triangularization theorem.
Theorem 7.1.1. [Generalized Schur’s Theorem] Let A ∈ Mn(ℂ). Suppose λ1,…,λk are the distinct eigenvalues of A with multiplicities m1,…,mk, respectively. Then, there exists a non-singular matrix W such that
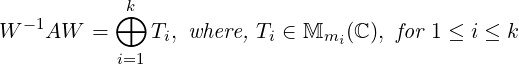
Proof. By Schur Upper Triangularization (see Lemma 6.2.12), there exists a unitary matrix U such that U*AU = T, an upper triangular matrix with diag(T) = (λ1,…,λ1,…,λk,…,λk).
Now, for any upper triangular matrix B, a real number α and i < j, consider the matrix F(B,i,j,α) = Eij(-α)BEij(α), where the matrix Eij(α) is defined in Definition 2.1.13. Then, for 1 ≤ k,ℓ ≤ n,
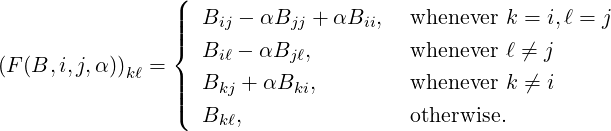 | (7.1.1) |
Now, using Equation (7.1.1), the diagonal entries of F(T,i,j,α) and T are equal and
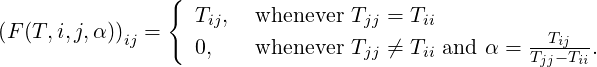
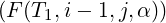 i-1,j = 0, for some choice of
α, whenever (T1)i-1,i-1≠Tjj. Moreover, this operation also preserves the 0 created by
F(T,i,j,α) at (i,j)-th place. Similarly, F(T1,i,j + 1,α) preserves the 0 created by F(T,i,j,α)
at (i,j)-th place. So, we can successively apply the following sequence of operations to
get
i-1,j = 0, for some choice of
α, whenever (T1)i-1,i-1≠Tjj. Moreover, this operation also preserves the 0 created by
F(T,i,j,α) at (i,j)-th place. Similarly, F(T1,i,j + 1,α) preserves the 0 created by F(T,i,j,α)
at (i,j)-th place. So, we can successively apply the following sequence of operations to
get
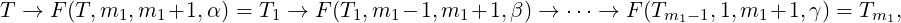
Exercise 7.1.2. Apply Theorem 7.1.1 to the matrix given below for better understanding.

 DRAFT
DRAFT
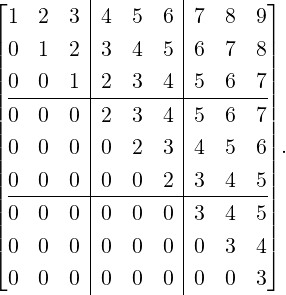
Definition 7.1.3. [Jordan Block and Jordan Matrix]
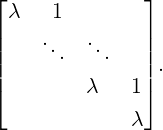

 DRAFT
DRAFT
We now give some examples of Jordan matrices with diagonal entries 0.
![[ ]
0](LA2260x.png) is the only Jordan matrix of size 1.
is the only Jordan matrix of size 1.
![[ ]
0 0
0 0](LA2261x.png) and J2(0) =
and J2(0) = ![[ ]
0 1
0 0](LA2262x.png) are Jordan matrices of size 2.
are Jordan matrices of size 2.
 , J
2(0) ⊕J1(0) =
, J
2(0) ⊕J1(0) =  and J
3(0) =
and J
3(0) =  are Jordan matrices of size 3.
are Jordan matrices of size 3.
We now give some properties of the Jordan blocks. The proofs are immediate and hence left for the reader. They will be used in the proof of subsequent results.
Remark 7.1.5. [Jordan blocks] Fix a positive integer k. Then,

 DRAFT
DRAFT
 .
.Definition 7.1.7. [Index of an Eigenvalue] Let J be a Jordan matrix containing Jt(λ), for some positive integer t and some complex number λ. Then, the smallest value of k for which Rank((J - λI)k) stops decreasing is the order of the largest Jordan block Jk(λ) in J. This number k is called the index of the eigenvalue λ.
Lemma 7.1.8. Let A ∈ Mn(ℂ) be strictly upper triangular. Then, A is similar to a direct sum of Jordan blocks. That is, there exists a non-singular matrix S and integers n1 ≥… ≥ nm ≥ 1 such that


 DRAFT
DRAFT
Proof. We will prove the result by induction on n. For n = 1, the statement is trivial. So, let the
result be true for matrices of size ≤ n - 1 and let A ∈ Mn(ℂ) be strictly upper triangular.
Then, A = ![[ T]
0 a
0 A1](LA2276x.png) . By induction hypothesis there exists an invertible matrix S1 such
that
. By induction hypothesis there exists an invertible matrix S1 such
that
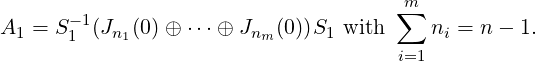
![⌊ ⌋
[ ] [ ] [ ][ T][ ] [ T ] 0 aT1 aT2
1 0 A 1 0 = 1 0 0 a 1 0 = 0 a S1 = |⌈0 Jn (0) 0|⌉,
0 S-11 0 S1 0 S-11 0 A1 0 S1 0 S-1A1S1 1
0 0 J](LA2280x.png)
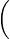 Jn1(0) ⊕
Jn1(0) ⊕ ⊕ Jnm(0)
⊕ Jnm(0)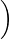 S1 = Jn1(0) ⊕ J and aT S1 =
S1 = Jn1(0) ⊕ J and aT S1 = ![[ ]
aT1 aT2](LA2284x.png) . Now, writing Jn1 to
mean Jn1(0) and using Remark 7.1.5.4e, we have
. Now, writing Jn1 to
mean Jn1(0) and using Remark 7.1.5.4e, we have
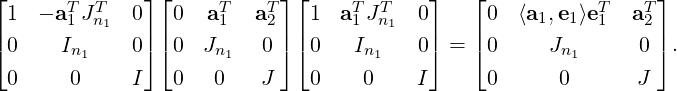

 DRAFT
is similar to
DRAFT
is similar to 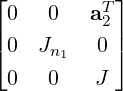 . This in turn is similar to
. This in turn is similar to 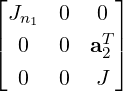 by permuting the first row and
column. At this stage, one can apply induction and if necessary do a block permutation, in order to
keep the block sizes in decreasing order.
by permuting the first row and
column. At this stage, one can apply induction and if necessary do a block permutation, in order to
keep the block sizes in decreasing order.
So, let us now assume that ⟨a1,e1⟩≠0. Then, writing α = ⟨a1,e1⟩, we have
![⌊ ⌋ ⌊ ⌋⌊ ⌋ ⌊ ⌋
1- 0 0 0 αeT1 aT2 α 0 0 0 eT1 aT2 [ ]
| α | | || | | | Jn1+1 e1aT2
⌈ 0 I 0 ⌉ ⌈0 Jn1 0 ⌉⌈ 0 I 0 ⌉ = ⌈0 Jn1 0⌉ ≡ 0 J .
0 0 1αI 0 0 J 0 0 αI 0 0 J](LA2290x.png)
![[ ][ ][ ] [ ]
I ei+1aT2Ji-1 Jn1+1 eiaT2 Ji- 1 I - ei+1aT2Ji-1 Jn1+1 ei+1aT2J i
= , for i ≥ 1.
0 I 0 J 0 I 0 J](LA2291x.png)
![[ ] [ ][ ][ ] [ ] [ ]
I ep+1aT2 Jp-1 I e2aT Jn1+1 e1aT I - e2aT I - ep+1aT Jp-1 Jn1+1 0
⋅⋅⋅ ⋅⋅⋅ = .
0 I 0 I 0 J 0 I 0 I 0 J](LA2292x.png)
Proof. Let λ1,…,λk be the distinct eigenvalues of A with algebraic multiplicities m1,…,mk. By Theorem 7.1.1, there exists a non-singular matrix S such that S-1AS = ⊕ i=1kTi, where Ti is an upper triangular with diagonal (λi,…,λi). Thus Ti - λiImi is a strictly upper triangular matrix. Thus, by Theorem 7.1.8, there exist a non-singular matrix Si such that
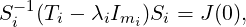
Now, take W = S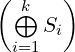 . Then, verify that W-1AW is a Jordan matrix. _
. Then, verify that W-1AW is a Jordan matrix. _
Let A ∈ Mn(ℂ). Suppose λ ∈ σ(A) and J is a Jordan matrix that is similar to A. Then, for each fixed i,1 ≤ i ≤ n, by ℓi(λ), we denote the number of Jordan blocks Jk(λ) in J for which k ≥ i. Then, the next result uses Exercise 7.1.6 to determine the number ℓi(λ).
Remark 7.1.11. Let A ∈ Mn(ℂ). Suppose λ ∈ σ(A) and J is a Jordan matrix that is similar
to A. Then, for 1 ≤ k ≤ n,

 DRAFT
DRAFT
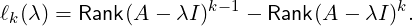
Proof. In view of Exercise 7.1.6, we need to consider only the Jordan blocks Jk(λ), for different values of k. Hence, without loss of generality, let us assume that J = ⊕ i=1naiJi(λ), where ai’s are non-negative integers and J contains exactly ai copies of the Jordan block Ji(λ), for 1 ≤ i ≤ n. Then, by definition and Exercise 7.1.6, we observe the following:
Thus, writing ℓi in place of ℓi(λ), we get
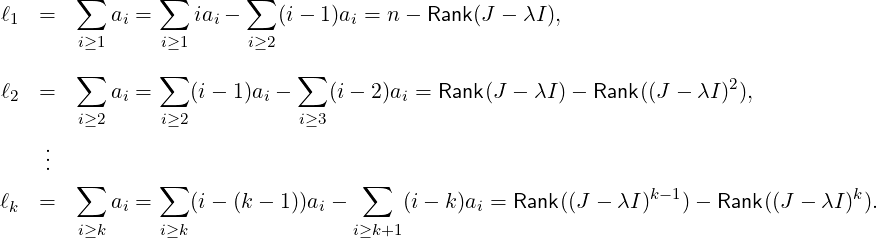

 DRAFT
DRAFT
Lemma 7.1.12. [Similar Jordan Matrices] Let J and J′ be two similar Jordan matrices of size n. Then, J is a block permutation of J′.
Proof. For 1 ≤ i ≤ n, let ℓi and ℓi′ be, respectively, the number of Jordan blocks of J and J′ of size at least i corresponding to λ. Since J and J′ are similar, the matrices (J -λI)i and (J′-λI)i are similar for all i,1 ≤ i ≤ n. Therefore, their ranks are equal for all i ≥ 1 and hence, ℓi = ℓi′ for all i ≥ 1. Thus the required result follows. _
We now state the main result of this section which directly follows from Lemma 6.2.12, Theorem 7.1.1 and Corollary 7.1.10 and hence the proof is omitted.
Theorem 7.1.13. [Jordan Canonical Form Theorem] Let A ∈ Mn(ℂ). Then, A is similar to a Jordan matrix J, which is unique up to permutation of Jordan blocks. If A ∈ Mn(ℝ) and has real eigenvalues then the similarity transformation matrix S may be chosen to have real entries. This matrix J is called the the Jordan canonical form of A, denoted Jordan CF(A).
We now start with a few examples and observations.
Example 7.1.14. Let us use the idea from Lemma 7.1.11 to find the Jordan Canonical Form of the following matrices.
 .
.
Solution: Note that ℓ1 = 4 -Rank(A - 0I) = 2. So, there are two Jordan blocks.
Also, ℓ2 = Rank(A - 0I) -Rank((A - 0I)2) = 2. So, there are at least 2 Jordan blocks of
size 2. As there are exactly two Jordan blocks, both the blocks must have size 2. Hence,
Jordan CF(A) = J2(0) ⊕ J2(0).

 DRAFT
DRAFT
 .
.
Solution: Let B = A1 - I. Then, ℓ1 = 4 -Rank(B) = 1. So, B has exactly one Jordan block and hence A1 is similar to J4(1).
 .
.
Solution: Let C = A2 - I. Then, ℓ1 = 4 -Rank(C) = 2. So, C has exactly two Jordan blocks. Also, ℓ2 = Rank(C) -Rank(C2) = 1 and ℓ3 = Rank(C2) -Rank(C3) = 1. So, there is at least 1 Jordan blocks of size 3.
Thus, we see that there are two Jordan blocks and one of them is of size 3. Also, the size of the matrix is 4. Thus, A2 is similar to J3(1) ⊕ J1(1).
Solution: One can directly get the answer from the previous exercises as the matrix A is already in the block diagonal form. But, we compute it again for better understanding.
Let B = A - I. Then, ℓ1 = 16 -Rank(B) = 5, ℓ2 = Rank(B) -Rank(B2) = 11 - 7 = 4, ℓ3 = Rank(B2) -Rank(B3) = 7 - 3 = 4 and ℓ4 = Rank(B3) -Rank(B4) = 3 - 0 = 3.
Hence, J4(1) appears thrice (as ℓ4 = 3 and ℓ5 = 0), J3(1) also appears once (as ℓ3-ℓ4 = 1), J2(1) does not appear as (as ℓ2 - ℓ3 = 0) and J1(1) appears once (as ℓ1 - ℓ2 = 1). Thus, the required result follows.
Remark 7.1.15. [Observations about Jordan CF(A)]
Łet λ1,…,λk be the distinct eigenvalues of A. Now, apply the Schur Upper Triangularization
Lemma (see Lemma 6.2.12) to get an upper triangular matrix, say T such that the diagonal
entries of T are λ1,…,λ1,λ2,…,λ2,…,λk,…,λk. Now, apply similarity transformations (see
Theorem 7.1.1) to get T = ⊕
i=1kTi, where each diagonal entry of Ti is λi. Then, for each

 DRAFT
i,1 ≤ i ≤ k, use Theorem 7.1.8 to get an invertible matrix Si such that Si-1(Ti-λiI)Si =
DRAFT
i,1 ≤ i ≤ k, use Theorem 7.1.8 to get an invertible matrix Si such that Si-1(Ti-λiI)Si =
 , a Jordan matrix. Thus, we obtain a Jordan matrix Ji =
, a Jordan matrix. Thus, we obtain a Jordan matrix Ji = 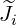 + λiI = Si-1TiSi, where
each diagonal entry of Ji is λi. Hence, S = ⊕
i=1kSi converts T = ⊕
i=1kTi into the
required Jordan matrix.
+ λiI = Si-1TiSi, where
each diagonal entry of Ji is λi. Hence, S = ⊕
i=1kSi converts T = ⊕
i=1kTi into the
required Jordan matrix.
![[ ]
ϵ 0
1 0](LA2314x.png) . Then, Aϵ is diagonalizable as A has distinct eigenvalues. So,
Jordan CF(Aϵ) =
. Then, Aϵ is diagonalizable as A has distinct eigenvalues. So,
Jordan CF(Aϵ) = ![[ ]
ϵ 0
0 0](LA2315x.png) .
.
Whereas, for A = ![[ ]
0 0
1 0](LA2316x.png) , we
know that Jordan CF(A) =
, we
know that Jordan CF(A) = ![[ ]
0 1
0 0](LA2317x.png) ≠limϵ→0Jordan CF(Aϵ). Thus, a small change in
the entries of A may change Jordan CF(A) significantly.
≠limϵ→0Jordan CF(Aϵ). Thus, a small change in
the entries of A may change Jordan CF(A) significantly.
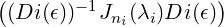 .
.
For if, A has at least ℓ + 1 linearly independent eigenvectors for λ, then dim(Null(A - λI)) > ℓ. So, Rank(A - λI) < n - ℓ. But, the number of Jordan blocks for λ in A is ℓ. Thus, we must have Rank(J - λI) = n - ℓ, a contradiction.
![[ ]
0](LA2319x.png) ⊕
⊕![[ ]
0 1
0 0](LA2320x.png) ⊕
⊕ and
and ![[ ]
0 1
0 0](LA2322x.png) ⊕
⊕![[ ]
0 1
0 0](LA2323x.png) ⊕
⊕![[ ]
0 1
0 0](LA2324x.png)

 DRAFT
are different Jordan CFs but they have the same algebraic and geometric multiplicities.
DRAFT
are different Jordan CFs but they have the same algebraic and geometric multiplicities.
![[ ]
ϵ](LA2327x.png) has rank 1 but it converges
to
has rank 1 but it converges
to ![[ ]
0](LA2328x.png) which has a different rank.
which has a different rank.Proof. Let Kn = 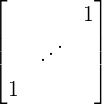 . Then, observe that K-1 = K and KJn(a)K = Jn(a)T , as the (i,j)-th
entry of A goes to (n - i + 1,n - j + 1)-th position in KAK. Hence,
. Then, observe that K-1 = K and KJn(a)K = Jn(a)T , as the (i,j)-th
entry of A goes to (n - i + 1,n - j + 1)-th position in KAK. Hence,
![[⊕ ] [⊕ ] [⊕ ] [⊕ ]T
Kni Jni(λi) Kni = Jni(λi) .](LA2330x.png)
We start this section with the following definition. Recall that a polynomial p(x) = a0 + a1x +  + anxn
with an = 1 is called a monic polynomial.
+ anxn
with an = 1 is called a monic polynomial.

 DRAFT
Definition 7.2.1. [Companion Matrix] Let P(t) = tn + an-1tn-1 +
DRAFT
Definition 7.2.1. [Companion Matrix] Let P(t) = tn + an-1tn-1 +  + a0 be a monic
polynomial in t of degree n. Then, the n×n matrix A =
+ a0 be a monic
polynomial in t of degree n. Then, the n×n matrix A =  , denoted
A(n : a0,…,an-1) or Companion(P), is called the companion matrix of P(t).
, denoted
A(n : a0,…,an-1) or Companion(P), is called the companion matrix of P(t).
Definition 7.2.2. [Annihilating Polynomial] Let A ∈ Mn(ℂ). Then, the polynomial P(t) is said to annihilate (destroy) A if P(A) = 0.
Let P(x) be the characteristic polynomial of A. Then, by the Cayley-Hamilton Theorem, P(A) = 0. So, if f(x) = P(x)g(x), for any multiple of g(x), then f(A) = P(A)g(A) = 0g(A) = 0. Thus, there are infinitely many polynomials which annihilate A. In this section, we will concentrate on a monic polynomial of least positive degree that annihilates A.
Definition 7.2.3. [Minimal polynomial] Let A ∈ Mn(ℂ). Then, the minimal polynomial of A, denoted mA(x), is a monic polynomial of least positive degree satisfying mA(A) = 0.
Theorem 7.2.4. Let A be the companion matrix of the monic polynomial P(t) = tn +
an-1tn-1 +  + a0. Then, P(t) is both the characteristic and the minimal polynomial of A.
+ a0. Then, P(t) is both the characteristic and the minimal polynomial of A.
Proof. Expanding det(tIn - Companion(P)) along the first row, we have

 DRAFT
DRAFT
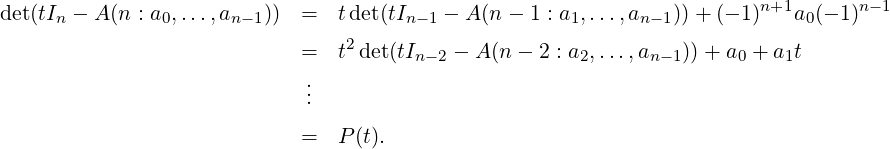
We will now show that P(t) is the minimal polynomial of A. To do so, we first observe that Ae1 = e2,…,Aen-1 = en. That is,
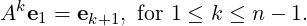 | (7.2.1) |
Now, Suppose we have a monic polynomial Q(t) = tm + bm-1tm-1 +  + b0, with m < n, such
that Q(A) = 0. Then, using Equation (7.2.1), we get
+ b0, with m < n, such
that Q(A) = 0. Then, using Equation (7.2.1), we get


 DRAFT
DRAFT
The next result gives us the existence of such a polynomial for every matrix A. To do so, recall that the well-ordering principle implies that if S is a subset of natural numbers then it contains a least element.
Lemma 7.2.5. [Existence of the Minimal Polynomial] Let A ∈ Mn(ℂ). Then, there exists a unique monic polynomial m(x) of minimum (positive) degree such that m(A) = 0. Further, if f(x) is any polynomial with f(A) = 0 then m(x) divides f(x).
Proof. Let P(x) be the characteristic polynomial of A. Then, deg(P(x)) = n and by the Cayley-Hamilton Theorem, P(A) = 0. So, consider the set
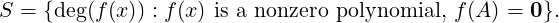
Also, without loss of generality, we can assume that m(x) is monic and unique (non-uniqueness will lead to a polynomial of smaller degree in S).
Now, suppose there is a polynomial f(x) such that f(A) = 0. Then, by division algorithm, there exist polynomials q(x) and r(x) such that f(x) = m(x)q(x) + r(x), where either r(x) is identically the zero polynomial of deg(r(x)) < M = deg(m(x)). As
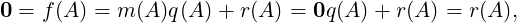
As an immediate corollary, we have the following result.

 DRAFT
DRAFT
Corollary 7.2.6. [Minimal polynomial divides the Characteristic Polynomial] Let mA(x) and PA(x) be, respectively, the minimal and the characteristic polynomials of A ∈ Mn(ℂ).
Proof. The first part following directly from Lemma 7.2.5. For the second part, let (λ,x) be an eigen-pair. Then, f(A)x = f(λ)x, for any polynomial of f, implies that
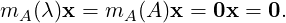
we also have the following result.
Proof. Since A and B are similar, there exists an invertible matrix S such that A = S-1BS. Hence, f(A) = F(S-1BS) = S-1f(B)S, for any polynomial f. Hence, mA(A) = 0 if and only if mA(B) = 0 and thus the required result follows. _

 DRAFT
Theorem 7.2.8. Let A ∈ Mn(ℂ) and let λ1,…,λk be the distinct eigenvalues of A. If ni is the
size of the largest Jordan block for λi in J = Jordan CFA then
DRAFT
Theorem 7.2.8. Let A ∈ Mn(ℂ) and let λ1,…,λk be the distinct eigenvalues of A. If ni is the
size of the largest Jordan block for λi in J = Jordan CFA then
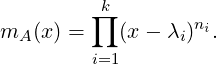
Proof. Using 7.2.6, we see that mA(x) = ∏
i=1k(x-λi)αi, for some αi’s with 1 ≤ αi ≤ Alg.Mulλ
i(A).
As mA(A) = 0, using Lemma 7.2.7 we have mA(J) = ∏
i=1k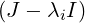 αi = 0. But, observe that for
the Jordan block Jni(λi), one has
αi = 0. But, observe that for
the Jordan block Jni(λi), one has
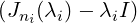 αi = 0 if and only if αi ≥ ni, and
αi = 0 if and only if αi ≥ ni, and
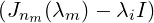 αi is invertible, for all m≠i.
αi is invertible, for all m≠i.Thus ∏ i=1k(J - λiI)ni = 0 and ∏i=1k(x - λi)ni divides ∏i=1k(x - λi)αi = mA(x) and ∏ i=1k(x - λi)ni is a monic polynomial, the result follows. _
As an immediate consequence, we also have the following result which corresponds to the converse of the above theorem.
Theorem 7.2.9. Let A ∈ Mn(ℂ) and let λ1,…,λk be the distinct eigenvalues of A. If the minimal polynomial of A equals ∏ i=1k(x - λi)ni then ni is the size of the largest Jordan block for λi in J = Jordan CFA.
Proof. It directly follows from Theorem 7.2.8. _
We now give equivalent conditions for a square matrix to be diagonalizable.
Proof. Part 1 ⇒ Part 2. If A is diagonalizable, then each Jordan block in J = Jordan CFA has size 1. Hence, by Theorem 7.2.8, mA(x) = ∏ i=1k(x - λi), where λi’s are the distinct eigenvalues of A.
Part 2 ⇒ Part 3. Let mA(x) = ∏
i=1k(x-λi), where λi’s are the distinct eigenvalues of A. Then,
mA(x) = 0 if and only if x = λi, for some i,1 ≤ i ≤ k. In that case, it is easy to verify that
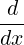 mA(x)≠0, for each λi.
mA(x)≠0, for each λi.
Part 3 ⇒ Part 1. Suppose that for each α satisfying mA(α) = 0, one has 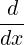 mA(α)≠0. Then, it
follows that each zero of mA(x) has multiplicity 1. Also, using Corollary 7.2.6, each zero of mA(x) is
an eigenvalue of A and hence by Theorem 7.2.8, the size of each Jordan block is 1. Thus, A is
diagonalizable. _
mA(α)≠0. Then, it
follows that each zero of mA(x) has multiplicity 1. Also, using Corollary 7.2.6, each zero of mA(x) is
an eigenvalue of A and hence by Theorem 7.2.8, the size of each Jordan block is 1. Thus, A is
diagonalizable. _
We now have the following remarks and observations.
Proof. Let B = Companion (f). Then, using Lemma 7.2.7, we see that mA(x) = mB(x). But, by Remark 7.2.11.1, we get mB(x) = f(x) and hence the required result follows.
Conversely, assume that mA(x) = f(x). But, by Remark 7.2.11.1, mB(x) = f(x) = PB(x), the characteristic polynomial of B. Since mA(x) = mB(x), the matrices A and B have the same largest Jordan blocks for each eigenvalue λ. As PB = mB, we know that for each λ, there is only one Jordan block in Jordan CFB. Thus, Jordan CFA = Jordan CFB and hence A is similar to Companion (f). _

 DRAFT
DRAFT
Exercise 7.2.12. The following are some facts and questions.
![[ ]
0 1
0 0](LA2365x.png) and B =
and B = ![[ ]
0 0
0 1](LA2366x.png) to verify that mAB(x)≠mBA(x).
to verify that mAB(x)≠mBA(x).We end this section with a method to compute the minimal polynomial of a given matrix.

 DRAFT
Example 7.2.13. [Computing the Minimal Polynomial] Let λ1,…,λk be the distinct
eigenvalues of A ∈ Mn(ℂ).
DRAFT
Example 7.2.13. [Computing the Minimal Polynomial] Let λ1,…,λk be the distinct
eigenvalues of A ∈ Mn(ℂ).
In the last section, we say that the matrices if A is a square matrix then A and AT are similar. In this section, we look at some more applications of the Jordan Canonical Form.
Consider the first order Initial Value Problem (IVP) x′(t) =  = A
= A = Ax(t), with
x(0) = 0. If A is not a diagonal matrix then the system is called coupled and is hard to solve. Note
that if A can be transformed to a nearly diagonal matrix, then the amount of coupling among xi’s can
be reduced. So, let us look at J = Jordan CF(A) = S-1AS. Then, using S-1A = JS-1. verify that
the initial problem x′(t) = Ax(t) is equivalent to the equation S-1x′(t) = S-1Ax(t) which
in turn is equivalent to y′(t) = Jy(t), where S-1x(t) = y(t) with y(0) = S-1x(0) = 0.
Therefore, if y is a solution to the second equation then x(t) = Sy is a solution to the initial
problem.
= Ax(t), with
x(0) = 0. If A is not a diagonal matrix then the system is called coupled and is hard to solve. Note
that if A can be transformed to a nearly diagonal matrix, then the amount of coupling among xi’s can
be reduced. So, let us look at J = Jordan CF(A) = S-1AS. Then, using S-1A = JS-1. verify that
the initial problem x′(t) = Ax(t) is equivalent to the equation S-1x′(t) = S-1Ax(t) which
in turn is equivalent to y′(t) = Jy(t), where S-1x(t) = y(t) with y(0) = S-1x(0) = 0.
Therefore, if y is a solution to the second equation then x(t) = Sy is a solution to the initial
problem.
When J is diagonalizable then solving the second is as easy as solving yi′(t) = λiyi(t) for which the required solution is given by yi(t) = yi(0)eλit.
If J is not diagonal, then for each Jordan block, the system reduces to
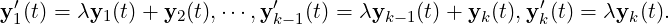

 DRAFT
DRAFT
Let P(x) be a polynomial and A ∈ Mn(ℂ). Then, P(A)A = AP(A). What about the converse? That is, suppose we are given that AB = BA for some B ∈ Mn(ℂ). Does it necessarily imply that B = P(A), for some nonzero polynomial P(x)? The answer is No as I commutes with A for every A. We start with a set of remarks.
Theorem 7.3.1. Let A ∈ Mn(ℂ) and B ∈ Mm(ℂ). Then, the linear system AX -XB = 0, in the variable matrix X of size n×m, has a unique solution, namely X = 0 (the trivial solution), if and only if σ(A) and σ(B) are disjoint.
Proof. Let us assume that σ(A) and σ(B) are disjoint.
Since σ(A) and σ(B) are disjoint, the matrix PB(A) = ![( )
∏
[λI - A ]
λ∈σ(B)](LA2374x.png) , obtained by evaluating
A at the characteristic polynomial, PB(t), of B, is invertible. So, let us look at the implication of the
condition AX = XB. This condition implies that A2X = AXB = XBB = XB2 and hence,
P(A)X = XP(B), for any polynomial P(t). In particular, PB(A)X = XPB(B) = X0 = 0. As PB(A)
is invertible, we get X = 0.
, obtained by evaluating
A at the characteristic polynomial, PB(t), of B, is invertible. So, let us look at the implication of the
condition AX = XB. This condition implies that A2X = AXB = XBB = XB2 and hence,
P(A)X = XP(B), for any polynomial P(t). In particular, PB(A)X = XPB(B) = X0 = 0. As PB(A)
is invertible, we get X = 0.
Now, conversely assume that AX - XB = 0 has only the trivial solution X = 0. Suppose on the contrary λ is a common eigenvalue of both A and B. So, choose nonzero vectors x ∈ ℂn and y ∈ ℂm such that (λ,x) is an eigen-pair of A and (λ,y) is a left eigen-pair of B. Now, define X0 = xyT . Then, X0 is an n × m nonzero matrix and
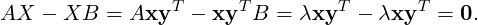
Corollary 7.3.2. Let A ∈ Mn(ℂ),B ∈ Mm(ℂ) and C be an n × m matrix. Also, assume that

 DRAFT
σ(A) and σ(B) are disjoint. Then, it can be easily verified that the system AX - XB = C, in
the variable matrix X of size n × m, has a unique solution, for any given C.
DRAFT
σ(A) and σ(B) are disjoint. Then, it can be easily verified that the system AX - XB = C, in
the variable matrix X of size n × m, has a unique solution, for any given C.
Proof. Consider the linear transformation T : Mn,m(ℂ) → Mn,m(ℂ), defined by T(X) = AX - XB. Then, by Theorem 7.3.1, Null(T) = {0}. Hence, by the rank-nullity theorem, T is a bijection and the required result follows. _
Definition 7.3.3. [Toeplitz Matrix] A square matrix A is said to be of Toeplitz type if each
(super/sub)-diagonal of A consists of the same element. For example, A = 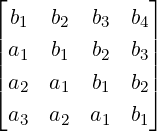 is a 4 × 4 Toeplitz type matrix. and the matrix B =
is a 4 × 4 Toeplitz type matrix. and the matrix B = 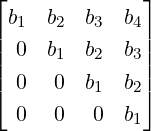 is an upper triangular
Toeplitz type matrix.
is an upper triangular
Toeplitz type matrix.
Exercise 7.3.4. Let Jn(0) ∈ Mn(ℂ) be the Jordan block with 0 on the diagonal.
 + anJn(0)n-1.
+ anJn(0)n-1.

 DRAFT
DRAFT
To proceed further, recall that a matrix A ∈ Mn(ℂ) is called non-derogatory if Geo.Mulα(A) = 1, for each α ∈ σ(A) (see Definition 6.2.4).
Theorem 7.3.5. Let A ∈ Mn(ℂ) be a non-derogatory matrix. Then, the matrices A and B commute if and only if B = P(A), for some polynomial P(t) of degree at most n - 1.
Proof. If B = P(A), for some polynomial P(t), then A and B commute. Conversely, suppose that
AB = BA, σ(A) = {λ1,…,λk} and let J = Jordan CFA = S-1AS be the Jordan matrix of A.
Then, J = 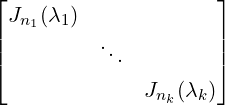 . Now, write B = S-1BS =
. Now, write B = S-1BS = 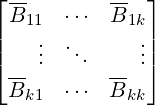 , where
B is partitioned conformally with J. Note that AB = BA gives JB = BJ. Thus, verify
that
, where
B is partitioned conformally with J. Note that AB = BA gives JB = BJ. Thus, verify
that
![Jn (λ1)B12 = [JB ]12 = [BJ ]12 = B12Jn (λ2),
1 2](LA2385x.png)
To proceed further, for 1 ≤ i ≤ k, define Fi(t) = ∏ j≠i(t-λj)nj. Then, Fi(t) is a polynomial with deg(Fi(t)) = n - ni and Fi(Jnj(λj)) = 0 if j≠i. Also, note that Fi(Jni(λi)) is a nonsingular upper triangular Toeplitz type matrix. Hence, its inverse has the same form and using Exercise 7.3.4.1, the matrix Fi(Jni(λi))-1Bii is also a Toeplitz type upper triangular matrix. Hence,

 DRAFT
DRAFT

 + Pk, we have
+ Pk, we have 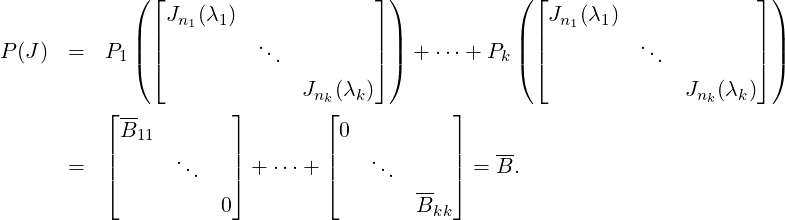

 DRAFT
DRAFT

 DRAFT
DRAFT

 DRAFT
DRAFT