
 DRAFT
Definition 5.1.3. [Inner Product Space] Let V be a vector space with an inner product ⟨,⟩.
Then, (V,⟨,⟩) is called an inner product space (in short, ips).
DRAFT
Definition 5.1.3. [Inner Product Space] Let V be a vector space with an inner product ⟨,⟩.
Then, (V,⟨,⟩) is called an inner product space (in short, ips).
Recall the dot product in ℝ2 and ℝ3. Dot product helped us to compute the length of vectors and angle between vectors. This enabled us to rephrase geometrical problems in ℝ2 and ℝ3 in the language of vectors. We generalize the idea of dot product to achieve similar goal for a general vector space over ℝ or ℂ. So, in this chapter F will denote either ℝ or ℂ.
Definition 5.1.1. [Inner Product] Let V be a vector space over F. An inner product over V, denoted by ⟨,⟩, is a map from V × V to F satisfying
Remark 5.1.2. Using the definition of inner product, we immediately observe that

 DRAFT
Definition 5.1.3. [Inner Product Space] Let V be a vector space with an inner product ⟨,⟩.
Then, (V,⟨,⟩) is called an inner product space (in short, ips).
DRAFT
Definition 5.1.3. [Inner Product Space] Let V be a vector space with an inner product ⟨,⟩.
Then, (V,⟨,⟩) is called an inner product space (in short, ips).
Example 5.1.4. Examples 1 and 2 that appear below are called the standard inner product or the dot product on ℝn and ℂn, respectively. Whenever an inner product is not clearly mentioned, it will be assumed to be the standard inner product.
 + unvn = vT u.
Then, ⟨,⟩ is indeed an inner product and hence
+ unvn = vT u.
Then, ⟨,⟩ is indeed an inner product and hence  ℝn,⟨,⟩
ℝn,⟨,⟩ is an ips.
is an ips.
 +unvn = v*u. Then,
+unvn = v*u. Then,
 ℂn,⟨,⟩
ℂn,⟨,⟩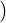 is an ips.
is an ips.
![[ ]
4 - 1
- 1 2](LA1352x.png) , define ⟨x,y⟩ = yT Ax. Then,
⟨,⟩ is an inner product as ⟨x,x⟩ = (x1 - x2)2 + 3x12 + x22.
, define ⟨x,y⟩ = yT Ax. Then,
⟨,⟩ is an inner product as ⟨x,x⟩ = (x1 - x2)2 + 3x12 + x22.
![[ ]
a b
b c](LA1353x.png) with a,c > 0 and ac > b2. Then, ⟨x,y⟩ = yT Ax is an inner product on
ℝ2 as ⟨x,x⟩ = ax12 + 2bx1x2 + cx22 = a
with a,c > 0 and ac > b2. Then, ⟨x,y⟩ = yT Ax is an inner product on
ℝ2 as ⟨x,x⟩ = ax12 + 2bx1x2 + cx22 = a![[ bx ]
x1 + -a2](LA1354x.png) 2 +
2 + 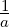
![[ 2]
ac - b](LA1356x.png) x22.
x22.

 DRAFT
DRAFT
 [-1,1] and define ⟨f,g⟩ = ∫
-11f(x)g(x)dx. Then,
[-1,1] and define ⟨f,g⟩ = ∫
-11f(x)g(x)dx. Then,
 = [u1,…,un] of a complex vector space V. Then, for any
u,v ∈ V, with [u]
= [u1,…,un] of a complex vector space V. Then, for any
u,v ∈ V, with [u] =
=  and [v]
and [v] =
=  , define ⟨u,v⟩ = ∑
i=1naibi. Then,
⟨,⟩ is indeed an inner product in V. So, any finite dimensional vector space can be
endowed with an inner product.
, define ⟨u,v⟩ = ∑
i=1naibi. Then,
⟨,⟩ is indeed an inner product in V. So, any finite dimensional vector space can be
endowed with an inner product.
 DRAFT
DRAFT
As ⟨u,u⟩ > 0, for all u≠0, we use inner product to define length of a vector.
Definition 5.1.5. [Length / Norm of a Vector] Let V be a vector space over F. Then, for
any vector u ∈ V, we define the length (norm) of u, denoted ∥u∥ = 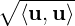 , the positive
square root. A vector of norm 1 is called a unit vector. Thus,
, the positive
square root. A vector of norm 1 is called a unit vector. Thus, 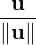 is called the unit vector
in the direction of u.
is called the unit vector
in the direction of u.

 DRAFT
DRAFT
 ∥x∥2 + ∥y∥2
∥x∥2 + ∥y∥2 , for all xT ,yT ∈ ℝn. This equality is
called the Parallelogram Law as in a parallelogram the sum of square of the lengths
of the diagonals is equal to twice the sum of squares of the lengths of the sides.
, for all xT ,yT ∈ ℝn. This equality is
called the Parallelogram Law as in a parallelogram the sum of square of the lengths
of the diagonals is equal to twice the sum of squares of the lengths of the sides.
 .
.
![[ ]
a b
b c](LA1378x.png) and define ⟨x,y⟩ = yT Ax.
Use given conditions to get a linear system of 3 equations in the variables a,b,c.]
and define ⟨x,y⟩ = yT Ax.
Use given conditions to get a linear system of 3 equations in the variables a,b,c.]
A very useful and a fundamental inequality, commonly called the Cauchy-Schwartz inequality, concerning the inner product is proved next.
Theorem 5.1.8 (Cauchy-Bunyakovskii-Schwartz inequality). Let V be an inner product space over F. Then, for any u,v ∈ V

 DRAFT
DRAFT
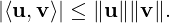 | (5.1.1) |
Moreover, equality holds in Inequality (5.1.1) if and only if u and v are linearly dependent.
Furthermore, if u≠0 then v = 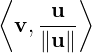
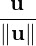 .
.
Proof. If u = 0 then Inequality (5.1.1) holds. Hence, let u≠0. Then, by Definition 5.1.1.3,
⟨λu + v,λu + v⟩≥ 0 for all λ ∈ F and v ∈ V. In particular, for λ = -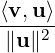 ,
,
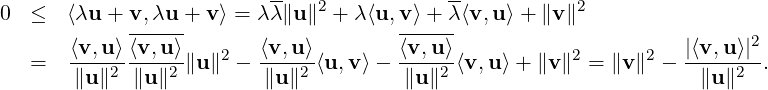
Now, note that equality holds in Inequality (5.1.1) if and only if ⟨λu + v,λu + v⟩ = 0, or equivalently, λu + v = 0. Hence, u and v are linearly dependent. Moreover,
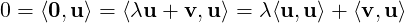
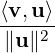 u =
u = 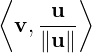
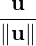 . _
. _
Let V be a real vector space. Then, for u,v ∈ V, the Cauchy-Schwartz inequality implies that
-1 ≤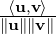 ≤ 1. We use this together with the properties of the cosine function to define the angle
between two vectors in an inner product space.
≤ 1. We use this together with the properties of the cosine function to define the angle
between two vectors in an inner product space.
Definition 5.1.10. [Angle between Vectors] Let V be a real vector space. If θ ∈ [0,π] is the angle between u,v ∈ V \{0} then we define
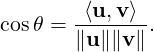
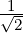 . So θ = π∕4.
. So θ = π∕4.
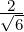 .
.
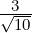 .
.

 DRAFT
DRAFT
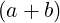
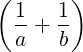 ≥ 4.
≥ 4.
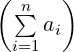
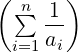 ≥ n2.
≥ n2.
 + zn| ≤
+ zn| ≤ 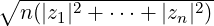 , for z1,…,zn ∈ ℂ. When does the
equality hold?
, for z1,…,zn ∈ ℂ. When does the
equality hold?
We will now prove that if A,B and C are the vertices of a triangle (see Figure 5.1) and a,b and c,
respectively, are the lengths of the corresponding sides then cos(A) = 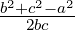 . This in turn implies
that the angle between vectors has been rightly defined.
. This in turn implies
that the angle between vectors has been rightly defined.
Lemma 5.1.12. Let A,B and C be the vertices of a triangle (see Figure 5.1) with corresponding side lengths a,b and c, respectively, in a real inner product space V then
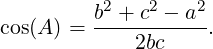
Proof. Let 0, u and v be the coordinates of the vertices A,B and C, respectively, of the triangle ABC.
Then, 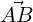 = u,
= u,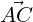 = v and
= v and 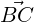 = v - u. Thus, we need to prove that
= v - u. Thus, we need to prove that
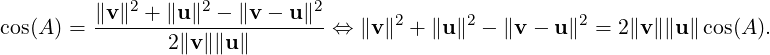
Definition 5.1.13. [Orthogonality / Perpendicularity] Let V be an inner product space over ℝ.
Then,

 DRAFT
DRAFT

 DRAFT
DRAFT
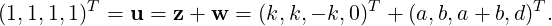
 (1,1,-1,0)T and w =
(1,1,-1,0)T and w =  (2,2,4,3)T .
(2,2,4,3)T .

 DRAFT
DRAFT
 = (2,1,3)T - (1,1,1)T = (1,0,2)T ,
= (2,1,3)T - (1,1,1)T = (1,0,2)T , 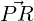 = (-2,0,1)T and
= (-2,0,1)T and
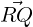 = (-3,0,-1)T . As ⟨
= (-3,0,-1)T . As ⟨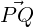 ,
,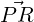 ⟩ = 0, the angle between the sides PQ and PR is
⟩ = 0, the angle between the sides PQ and PR is
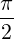 .
.
Method 2: ∥PQ∥ = 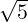 ,∥PR∥ =
,∥PR∥ = 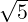 and ∥QR∥ =
and ∥QR∥ = 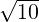 . As ∥QR∥2 = ∥PQ∥2 + ∥PR∥2, by
Pythagoras theorem, the angle between the sides PQ and PR is
. As ∥QR∥2 = ∥PQ∥2 + ∥PR∥2, by
Pythagoras theorem, the angle between the sides PQ and PR is 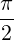 .
.

 DRAFT
DRAFT
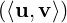 = π∕3, where u = (1,-1,1)T and v = (1,k,1)T .
= π∕3, where u = (1,-1,1)T and v = (1,k,1)T .
 and
and  .
.
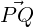 and
and 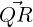 with ∥x∥ =
with ∥x∥ = 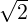 .
.
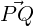 and
and 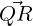 and x, where x is one
of the vectors found in Part 3d. Do you think the volume would be different if you
choose the other vector x?
and x, where x is one
of the vectors found in Part 3d. Do you think the volume would be different if you
choose the other vector x?
 DRAFT
DRAFT
To proceed further, recall that a vector space over ℝ or ℂ was a linear space.
Definition 5.1.16. [Normed Linear Space] Let V be a linear space.
Proof. As ∥x∥ = ∥x - y + y∥≤∥x - y∥ + ∥y∥ one has ∥x∥-∥y∥≤∥x - y∥. Similarly, one obtains ∥y∥-∥x∥≤∥y - x∥ = ∥x - y∥. Combining the two, the required result follows. _
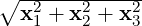 is a norm. Also, observe that this norm corresponds to
is a norm. Also, observe that this norm corresponds to
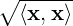 , where ⟨,⟩ is the standard inner product.
, where ⟨,⟩ is the standard inner product.
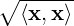 is a norm?
is a norm? 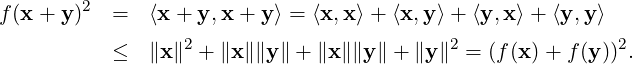
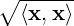 is a norm, called the norm induced by the inner product ⟨⋅,⋅⟩.
is a norm, called the norm induced by the inner product ⟨⋅,⋅⟩.The next result is stated without proof as the proof is beyond the scope of this book.
Theorem 5.1.20. Let ∥⋅∥ be a norm on a nls V. Then, ∥⋅∥ is induced by some inner product if and only if ∥⋅∥ satisfies the parallelogram law: ∥x + y∥2 + ∥x - y∥2 = 2∥x∥2 + 2∥y∥2.

 DRAFT
DRAFT
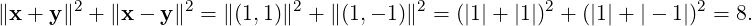
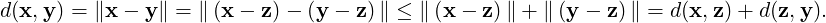
We start with the definition of an orthonormal set.
Definition 5.2.1. Let V be an ips. Then, a non-empty set S = {v1,…,vn}⊆ V is called an
orthogonal set if vi and vj are mutually orthogonal, for 1 ≤ i≠j ≤ n, i.e.,

 DRAFT
DRAFT
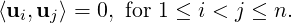
Further, if ∥vi∥ = 1, for 1 ≤ i ≤ n, Then S is called an orthonormal set. If S is also a basis of V then S is called an orthonormal basis of V.
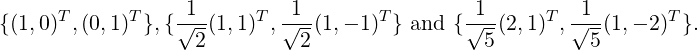
![{ }
[-1- -1- 1-]T [ 1---1-]T [-2- -1- -1]T
√3,- √3, √3 , 0,√2,√2- , √6-,√6,- √6](LA1473x.png) is an orthonormal set in
ℝ3.
is an orthonormal set in
ℝ3.

 DRAFT
DRAFT
 [-π,π].
Consider S = {1}∪{em|m ≥ 1}∪{fn|n ≥ 1}, where 1(x) = 1, em(x) = cos(mx) and
fn(x) = sin(nx), for all m,n ≥ 1 and for all x ∈ [-π,π]. Then,
[-π,π].
Consider S = {1}∪{em|m ≥ 1}∪{fn|n ≥ 1}, where 1(x) = 1, em(x) = cos(mx) and
fn(x) = sin(nx), for all m,n ≥ 1 and for all x ∈ [-π,π]. Then,
Hence, 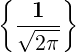 ∪
∪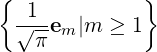 ∪
∪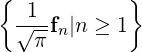 is an orthonormal set in
is an orthonormal set in  [-π,π].
[-π,π].
To proceed further, we consider a few examples for better understanding.
Example 5.2.3. Which point on the plane P is closest to the point, say Q?
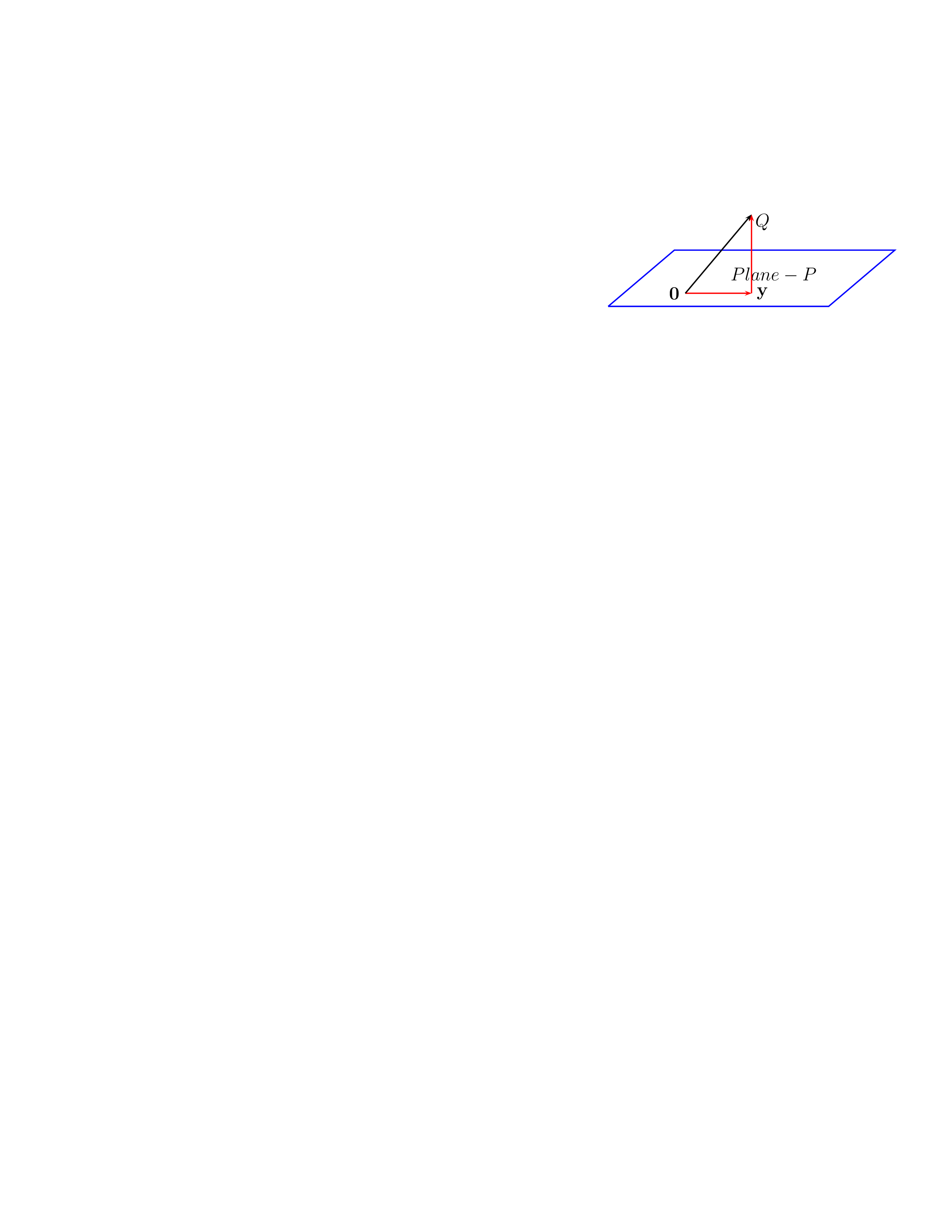
Solution: Let y be the foot of the perpendicular from Q on P. Thus, by Pythagoras Theorem, this point is unique. So, the question arises: how do we find y?
Note that 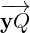 gives a normal vector of the plane P. Hence,
gives a normal vector of the plane P. Hence, 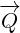 = y +
= y + 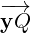 . So, need to decompose
. So, need to decompose 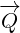 into two vectors such that one of them lies on the plane P and the other is orthogonal to the
plane.
into two vectors such that one of them lies on the plane P and the other is orthogonal to the
plane.
Thus, we see that given u,v ∈ V \{0}, we need to find two vectors, say y and z, such that y is parallel to u and z is perpendicular to u. Thus, y = ucos(θ) and z = usin(θ), where θ is the angle between u and v.
We do this as follows (see Figure 5.2). Let 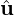 =
= 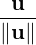 be the unit vector in the direction of u. Then,
using trigonometry, cos(θ) =
be the unit vector in the direction of u. Then,
using trigonometry, cos(θ) = 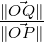 . Hence ∥
. Hence ∥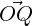 ∥ = ∥
∥ = ∥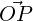 ∥cos(θ). Now using Definition 5.1.10,
∥
∥cos(θ). Now using Definition 5.1.10,
∥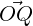 ∥ = ∥v∥
∥ = ∥v∥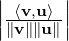 =
= 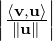 , where the absolute value is taken as the length/norm is a positive
quantity. Thus,
, where the absolute value is taken as the length/norm is a positive
quantity. Thus,
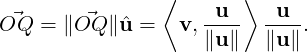
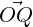 =
= 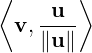
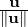 and z = v -
and z = v -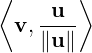
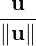 . In literature, the vector y =
. In literature, the vector y = 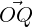 is
called the orthogonal projection of v on u, denoted Proju(v). Thus,
is
called the orthogonal projection of v on u, denoted Proju(v). Thus,
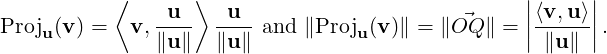 | (5.2.1) |
Moreover, the distance of u from the point P equals ∥ ∥ = ∥
∥ = ∥ ∥ =
∥ = 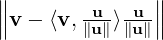 .
.

 DRAFT
DRAFT
Answer: (x,y,z,w) lies on the plane x-y-z+2w = 0 ⇔⟨(1,-1,-1,2),(x,y,z,w)⟩ = 0.
So, the required point equals
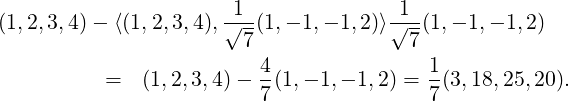
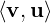
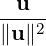 =
= 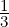 (1,1,-1,0)T and
w = (1,1,1,1)T - Projv(u) =
(1,1,-1,0)T and
w = (1,1,1,1)T - Projv(u) = 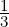 (2,2,4,3)T is orthogonal to u.
(2,2,4,3)T is orthogonal to u.
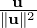 =
= 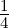 u =
u = 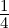 (1,1,1,1)T is parallel to u.
(1,1,1,1)T is parallel to u.
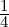 u =
u = 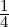 (3,3,-5,-1)T is orthogonal to u.
(3,3,-5,-1)T is orthogonal to u.Note that Proju(w) is parallel to u and Projv2(w) is parallel to v2. Hence, we have
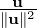 =
= 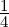 u =
u = 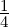 (1,1,1,1)T is parallel to u,
(1,1,1,1)T is parallel to u,
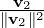 =
= 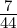 (3,3,-5,-1)T is parallel to v2 and
(3,3,-5,-1)T is parallel to v2 and
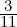 (1,1,2,-4)T is orthogonal to both u and v2.
(1,1,2,-4)T is orthogonal to both u and v2.
 DRAFT
DRAFT
We now prove the most important initial result of this section.
Theorem 5.2.5. Let S = {u1,…,un} be an orthonormal subset of an ips V(F).
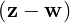 with ⟨z - w,w⟩ = 0, i.e.,
z - w ∈ LS(S)⊥. Further, ∥z∥2 = ∥w∥2 + ∥z - w∥2 ≥∥w∥2.
with ⟨z - w,w⟩ = 0, i.e.,
z - w ∈ LS(S)⊥. Further, ∥z∥2 = ∥w∥2 + ∥z - w∥2 ≥∥w∥2.
Proof. Part 1: Consider the linear system c1u1 +  + cnun = 0 in the variables c1,…,cn. As ⟨0,u⟩ = 0
and ⟨uj,ui⟩ = 0, for all j≠i, we have
+ cnun = 0 in the variables c1,…,cn. As ⟨0,u⟩ = 0
and ⟨uj,ui⟩ = 0, for all j≠i, we have
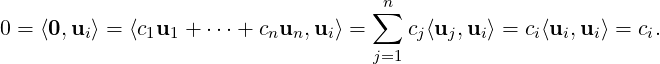
Part 2: Note that ⟨v,ui⟩ = ⟨∑ j=1nαjuj,ui⟩ = ∑ j=1nαj⟨uj,ui⟩ = αi⟨ui,ui⟩ = αi. This completes the first sub-part. For the second sub-part, we have

 DRAFT
DRAFT
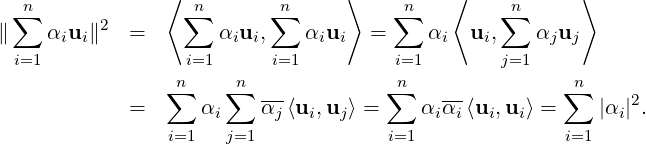
Part 3: Note that for 1 ≤ i ≤ n,
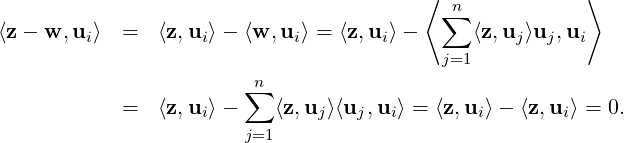
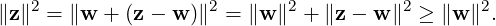
Part 4: Follows directly using Part 2b as {u1,…,un} is a basis of V. _
A rephrasing of Theorem 5.2.5.2b gives a generalization of the pythagoras theorem, popularly known as the Parseval’s formula. The proof is left as an exercise for the reader.

 DRAFT
Theorem 5.2.6. Let V be a finite dimensional ips with an orthonormal basis {v1,
DRAFT
Theorem 5.2.6. Let V be a finite dimensional ips with an orthonormal basis {v1, ,vn}.
Then, for each x,y ∈ V,
,vn}.
Then, for each x,y ∈ V,
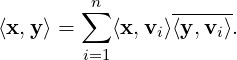
As a corollary to Theorem 5.2.5, we have the following result.
Theorem 5.2.7 (Bessel’s Inequality). Let V be an ips with {v1, ,vn} as an orthogonal
set. Then, ∑
k=1n
,vn} as an orthogonal
set. Then, ∑
k=1n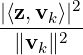 ≤ ∥z∥2, for each z ∈ V. Equality holds if and only if z =
∑
k=1n
≤ ∥z∥2, for each z ∈ V. Equality holds if and only if z =
∑
k=1n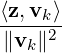 vk.
vk.
Proof. For 1 ≤ k ≤ n, define uk = 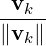 and use Theorem 5.2.5.4 to get the required result. _
and use Theorem 5.2.5.4 to get the required result. _
Remark 5.2.8. Using Theorem 5.2.5, we see that if  =
=  v1,…,vn
v1,…,vn![]](LA1545x.png) is an ordered orthonormal
basis of an ips V then for each u ∈ V, [u]
is an ordered orthonormal
basis of an ips V then for each u ∈ V, [u] =
= 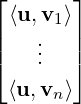 . Thus, in place of solving a linear
system to get the coordinates of a vector, we just need to compute the inner product with basis
vectors.
. Thus, in place of solving a linear
system to get the coordinates of a vector, we just need to compute the inner product with basis
vectors.
In view of the importance of Theorem 5.2.5, we inquire into the question of extracting an orthonormal basis from a given basis. The process of extracting an orthonormal basis from a finite linearly independent set is called the Gram-Schmidt Orthonormalization process. We first consider a few examples. Note that Theorem 5.2.5 also gives us an algorithm for doing so, i.e., from the given vector subtract all the orthogonal projections/components. If the new vector is nonzero then this vector is orthogonal to the previous ones. The proof follows directly from Theorem 5.2.5 but we give it again for the sake of completeness.
Theorem 5.2.10 (Gram-Schmidt Orthogonalization Process). Let V be an ips. If {v1,…,vn} is a set of linearly independent vectors in V then there exists an orthonormal set {w1,…,wn} in V. Furthermore, LS(w1,…,wi) = LS(v1,…,vi), for 1 ≤ i ≤ n.
Proof. Note that for orthonormality, we need ∥wi∥ = 1, for 1 ≤ i ≤ n and ⟨wi,wj⟩ = 0, for
1 ≤ i≠j ≤ n. Also, by Corollary 3.3.8.2, vi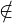 LS(v1,…,vi-1), for 2 ≤ i ≤ n, as {v1,…,vn} is a linearly
independent set. We are now ready to prove the result by induction.
LS(v1,…,vi-1), for 2 ≤ i ≤ n, as {v1,…,vn} is a linearly
independent set. We are now ready to prove the result by induction.
Step 1: Define w1 = 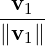 then LS(v1) = LS(w1).
then LS(v1) = LS(w1).
Step 2: Define u2 = v2 -⟨v2,w1⟩w1. Then, u2≠0 as v2 ⁄∈ LS(v1). So, let w2 = 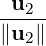 .
.
Note that {w1,w2} is orthonormal and LS(w1,w2) = LS(v1,v2).
Step 3: For induction, assume that we have obtained an orthonormal set {w1,…,wk-1} such that
LS(v1,…,vk-1) = LS(w1,…,wk-1). Now, note that
uk = vk -∑
i=1k-1⟨vk,wi⟩wi = vk -∑
i=1k-1Projwi(vk)≠0 as vk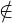 LS(v1,…,vk-1). So, let us put
wk =
LS(v1,…,vk-1). So, let us put
wk = 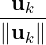 . Then, {w1,…,wk} is orthonormal as ∥wk∥ = 1 and
. Then, {w1,…,wk} is orthonormal as ∥wk∥ = 1 and

 DRAFT
DRAFT
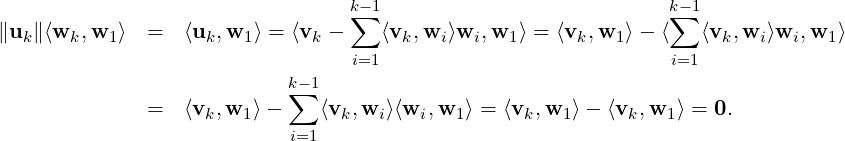
As vk = ∥uk∥wk + ∑ i=1k-1⟨vk,wi⟩wi, we get vk ∈ LS(w1,…,wk). Hence, by the principle of mathematical induction LS(w1,…,wk) = LS(v1,…,vk) and the required result follows. _
We now illustrate the Gram-Schmidt process with a few examples.
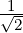 (1,0,1,0)T . As ⟨v2,w1⟩ = 0, we get w2 =
(1,0,1,0)T . As ⟨v2,w1⟩ = 0, we get w2 = 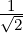 (0,1,0,1)T . For the third vector,
let u3 = v3 -⟨v3,w1⟩w1 -⟨v3,w2⟩w2 = (0,-1,0,1)T . Thus, w3 =
(0,1,0,1)T . For the third vector,
let u3 = v3 -⟨v3,w1⟩w1 -⟨v3,w2⟩w2 = (0,-1,0,1)T . Thus, w3 =  (0,-1,0,1)T .
(0,-1,0,1)T .
![[ ]
2 0 0](LA1565x.png) T ,v2 =
T ,v2 = ![[ ]
3 2 0
2](LA1566x.png) T ,v3 =
T ,v3 = ![[ ]
1 3 0
2 2](LA1567x.png) T ,v4 =
T ,v4 = ![[ ]
1 1 1](LA1568x.png) T }. Find
an orthonormal set T such that LS(S) = LS(T).
T }. Find
an orthonormal set T such that LS(S) = LS(T). 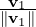 =
= ![[ ]
1 0 0](LA1570x.png) T = e1. For the second vector, consider
u2 = v2 -
T = e1. For the second vector, consider
u2 = v2 - w1 =
w1 = ![[ ]
0 2 0](LA1572x.png) T . So, put w2 =
T . So, put w2 = 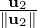 =
= ![[ ]
0 1 0](LA1574x.png) T = e2.
T = e2.
For the third vector, let u3 = v3 -∑ i=12⟨v3,wi⟩wi = (0,0,0)T . So, v3 ∈ LS((w1,w2)). Or equivalently, the set {v1,v2,v3} is linearly dependent.
So, for again computing the third vector, define u4 = v4 -∑ i=12⟨v4,wi⟩wi. Then, u4 = v4 - w1 - w2 = e3. So w4 = e3. Hence, T = {w1,w2,w4} = {e1,e2,e3}.
 (1,2,1),(x,y,z)
(1,2,1),(x,y,z) = 0. Thus,
= 0. Thus,
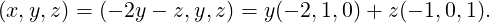
Method 1: Apply Gram-Schmidt process to {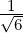 (1,2,1)T ,(-2,1,0)T ,(-1,0,1)T }⊆ ℝ3.
(1,2,1)T ,(-2,1,0)T ,(-1,0,1)T }⊆ ℝ3.
Method 2: Valid only in ℝ3 using the cross product of two vectors.
In either case, verify that {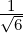 (1,2,1),
(1,2,1),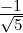 (2,-1,0),
(2,-1,0),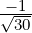 (1,2,-5)} is the required set.
(1,2,-5)} is the required set.
We now state two immediate corollaries without proof.
Corollary 5.2.12. Let V≠{0} be an ips. If
Remark 5.2.13. Let S = {v1,…,vn}≠{0} be a non-empty subset of a finite dimensional vector space V. If we apply Gram-Schmidt process to

 DRAFT
DRAFT
 = {v1,…,vn} as a basis. Then, prove that
= {v1,…,vn} as a basis. Then, prove that  is orthonormal if and
only if for each x ∈ V, x = ∑
i=1n⟨x,vi⟩vi. [Hint: Since
is orthonormal if and
only if for each x ∈ V, x = ∑
i=1n⟨x,vi⟩vi. [Hint: Since  is a basis, each x ∈ V has a
unique linear combination in terms of vi’s.]
is a basis, each x ∈ V has a
unique linear combination in terms of vi’s.]
 = {v1,…,vn} be an orthonormal set in ℝn. For 1 ≤ k ≤ n, define Ak =
∑
i=1kviviT . Then, prove that AkT = Ak and Ak2 = Ak. Thus, Ak’s are projection
matrices.
= {v1,…,vn} be an orthonormal set in ℝn. For 1 ≤ k ≤ n, define Ak =
∑
i=1kviviT . Then, prove that AkT = Ak and Ak2 = Ak. Thus, Ak’s are projection
matrices.
We end this section by proving the fundamental theorem of linear algebra. So, the readers are advised to recall the four fundamental subspaces and also to go through Theorem 3.5.9 (the rank-nullity theorem for matrices). We start with the following result.
Proof. Let x ∈ Null(A). Then, Ax = 0. So, (AT A)x = AT (Ax) = AT 0 = 0. Thus, x ∈ Null(AT A). That is, Null(A) ⊆ Null(AT A).
Suppose that x ∈ Null(AT A). Then, (AT A)x = 0 and 0 = xT 0 = xT (AT A)x = (Ax)T (Ax) = ∥Ax∥2. Thus, Ax = 0 and the required result follows. _
Proof. Part 1: Proved in Theorem 3.5.9.
Part 2: We first prove that Null(A) ⊆ Col(A*)⊥. Let x ∈ Null(A). Then, Ax = 0
and

 DRAFT
DRAFT
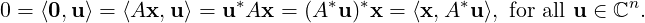
We now prove that Col(A*)⊥⊆ Null(A). Let x ∈ Col(A*)⊥. Then, for every y ∈ ℂn,
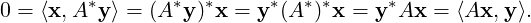
Part 3: Use the first two parts to get the required result.
Hence the proof of the fundamental theorem is complete. _
Remark 5.2.17. Theorem 5.2.16.2 implies that Null(A) =  Col(A*)
Col(A*)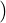 ⊥. This statement is
just stating the usual fact that if x ∈ Null(A) then Ax = 0 and hence the usual dot product of
every row of A with x equals 0.
⊥. This statement is
just stating the usual fact that if x ∈ Null(A) then Ax = 0 and hence the usual dot product of
every row of A with x equals 0.
As an implication of Theorem 5.2.16.2 and Theorem 5.2.16.3, we show the existence of an invertible linear map T : Col(A*) → Col(A).
Corollary 5.2.18. Let A ∈ Mn(ℂ). Then, the function T : Col(A*) → Col(A) defined by
T(x) = Ax is invertible.

 DRAFT
DRAFT
Proof. In view of Theorem 5.2.16.3 and the rank-nullity theorem, we just need to show that the map is one-one. So, suppose that there exist x,y ∈ Col(A*) such that T(x) = T(y). Or equivalently, Ax = Ay. Thus, x - y ∈ Null(A) = (Col(A*))⊥ (by Theorem 5.2.16.2). Therefore, x-y ∈ (Col(A*))⊥∩Col(A*) = {0}. Thus, x = y and hence the map is one-one. Thus, the required result follows. _
The readers should look at Example 3.2.3 and Remark 3.2.4. We give one more example.
Example 5.2.19. Let A = 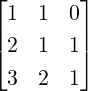 . Then, verify that
. Then, verify that

 DRAFT
DRAFT
For more information related with the fundamental theorem of linear algebra the interested readers are advised to see the article “The Fundamental Theorem of Linear Algebra, Gilbert Strang, The American Mathematical Monthly, Vol. 100, No. 9, Nov., 1993, pp. 848 - 855.”
The next result gives the proof of the QR decomposition for real matrices. The readers are advised to prove similar results for matrices with complex entries. This decomposition and its generalizations are helpful in the numerical calculations related with eigenvalue problems (see Chapter 6).
Theorem 5.2.1 (QR Decomposition). Let A ∈ Mn(ℝ) be invertible. Then, there exist matrices Q and R such that Q is orthogonal and R is upper triangular with A = QR. Furthermore, if det(A)≠0 then the diagonal entries of R can be chosen to be positive. Also, in this case, the decomposition is unique.
Proof. As A is invertible, it’s columns form a basis of ℝn. So, an application of the Gram-Schmidt orthonormalization process to {A[:,1],…,A[:,n]} gives an orthonormal basis {v1,…,vn} of ℝn satisfying
![LS (A [:,1],...,A[:,i]) = LS (v1,...,vi), for 1 ≤ i ≤ n.](LA1605x.png)

 DRAFT
DRAFT
Since A[:,i] ∈ LS(v1,…,vi), for 1 ≤ i ≤ n, there exist αji ∈ ℝ,1 ≤ j ≤ i, such that
A[:,i] = [v1,…,vi] . Thus, if Q = [v1,…,vn] and R =
. Thus, if Q = [v1,…,vn] and R =  then
then
Thus, this completes the proof of the first part. Note that
 LS(v1,…,vi-1).
LS(v1,…,vi-1).
Uniqueness: Suppose Q1R1 = Q2R2 for some orthogonal matrices Qi’s and upper triangular matrices Ri’s with positive diagonal entries. As Qi’s and Ri’s are invertible, we get Q2-1Q1 = R2R1-1. Now, using
So, the matrix R2R1-1 is an orthogonal upper triangular matrix and hence, by Exercise 1.2.11.4, R2R1-1 = In. So, R2 = R1 and therefore Q2 = Q1. _
Let A be an n × k matrix with Rank(A) = r. Then, by Remark 5.2.13, an application of the Gram-Schmidt orthonormalization process to columns of A yields an orthonormal set {v1,…,vr}⊆ ℝn such that
![LS (A [:,1],...,A [:,j]) = LS (v1,...,vi), for 1 ≤ i ≤ j ≤ k.](LA1611x.png)

 DRAFT
DRAFT
Theorem 5.2.2 (Generalized QR Decomposition). Let A be an n × k matrix of rank r. Then, A = QR, where
 . Find an orthogonal matrix Q and an upper triangular matrix
R such that A = QR.
. Find an orthogonal matrix Q and an upper triangular matrix
R such that A = QR. 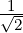 (1,0,1,0)T , w2 =
(1,0,1,0)T , w2 = 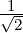 (0,1,0,1)T
and w3 =
(0,1,0,1)T
and w3 = 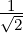 (0,-1,0,1)T . We now compute w4. If v4 = (2,1,1,1)T then
(0,-1,0,1)T . We now compute w4. If v4 = (2,1,1,1)T then
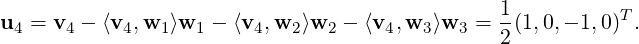
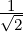 (-1,0,1,0)T . Hence, we see that A = QR with
(-1,0,1,0)T . Hence, we see that A = QR with  w1,…,w4
w1,…,w4![]](LA1621x.png) =
= 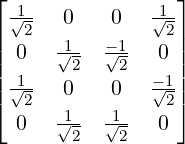 and R =
and R = 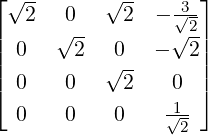 .
.
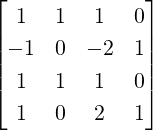 . Find a 4 × 3 matrix Q satisfying QT Q = I3 and an upper
triangular matrix R such that A = QR.
. Find a 4 × 3 matrix Q satisfying QT Q = I3 and an upper
triangular matrix R such that A = QR. 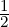 v1. Let v2 = (1,0,1,0)T . Then,
v1. Let v2 = (1,0,1,0)T . Then,
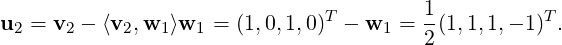
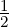 (1,1,1,-1)T . Let v3 = (1,-2,1,2)T . Then,
(1,1,1,-1)T . Let v3 = (1,-2,1,2)T . Then,
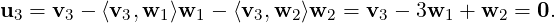
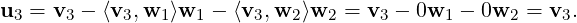
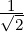 (0,1,0,1)T . Hence,
(0,1,0,1)T . Hence,

 DRAFT
DRAFT
![⌊ 1 1 ⌋
| 2 2 0 | ⌊2 1 3 0 ⌋
|| -21- 12 1√2|| | |
Q = [v1, v2,v3] = | 1 1 0 | and R = ⌈0 1 - 1 √0-⌉.
⌈ 21 -21 1 ⌉ 0 0 0 2
2 -2- √2-](LA1635x.png)
Remark 5.2.4. Let A ∈ Mm,n(ℝ).
![⌊ ⌋
⟨v1,A [:,1]⟩ ⟨v1,A [:,2]⟩ ⟨v1,A [:,3]⟩ ⋅⋅⋅
|| 0 ⟨v2,A [:,2]⟩ ⟨v2,A [:,3]⟩ ⋅⋅⋅||
| |
|⌈ 0 0 ⟨v3,A [:,3]⟩ ⋅⋅⋅|⌉
... ... ...](LA1636x.png) .
In case Rank(A) < n then a slight modification gives the matrix R.
.
In case Rank(A) < n then a slight modification gives the matrix R.

 DRAFT
DRAFT
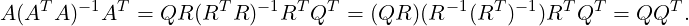
![⌊ ⌋
vT
| 1. | ∑n
P = A(AT A)-1AT = QQT = [v1,...,vn]|⌈ .. |⌉ = vivTi
vT i=1
n](LA1640x.png)

 DRAFT
DRAFT
Till now, our main interest was to understand the linear system Ax = b, for A ∈ Mm,n(ℂ),x ∈ ℂn and b ∈ ℂm, from different view points. But, in most practical situations the system has no solution. So, we are interested in finding a point x0 ∈ ℝn such that the err = b - Ax0 is the least. Thus, we consider the problem of finding x0 ∈ ℝn such that
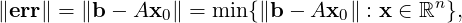
To begin with, recall the following result from Page §.
Theorem 5.3.1 (Decomposition). Let V be an ips having W as a finite dimensional subspace. Suppose {f1,…,fk} is an orthonormal basis of W. Then, for each b ∈ V, y = ∑ i=1k⟨b,fi⟩fi is the closest point in W from b. Furthermore, b - y ∈ W⊥.
We now give a definition and then an implication of Theorem 5.3.1.
Definition 5.3.2. [Orthogonal Projection] Let W be a finite dimensional subspace of an ips V. Then, by Theorem 5.3.1, for each v ∈ V there exist unique vectors w ∈ W and u ∈ W⊥ with v = w + u. We thus define the orthogonal projection of V onto W, denoted PW, by
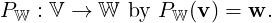
Remark 5.3.3. Let A ∈ Mm,n(ℝ) and W = Col(A). Then, to find the orthogonal projection PW(b), we can use either of the following ideas:
Before proceeding to projections, we give an application of Theorem 5.3.1 to a linear system.
Corollary 5.3.4. Let A ∈ Mm,n(ℝ) and b ∈ ℝm. Then, every least square solution of Ax = b is a solution of the system AT Ax = AT b. Conversely, every solution of AT Ax = AT b is a least square solution of Ax = b.
Proof. As b ∈ ℝm, by Remark 5.3.3, there exists y ∈ Col(A) and v ∈ Null(AT ) such that b = y + v and min{∥b-w∥|w ∈ Col(A)} = ∥b-y∥. As y ∈ Col(A), there exists x0 ∈ ℝn such that Ax0 = y, i.e., x0 is the least square solution of Ax = b. Hence,
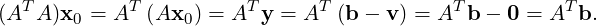

 DRAFT
DRAFT
Conversely, let x1 ∈ ℝn be a solution of AT Ax = AT b, i.e., AT 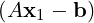 = 0. To
show
= 0. To
show
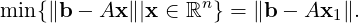
Note that AT (Ax1 - b) = 0 implies 0 = (x - x1)T AT (Ax1 - b) = (Ax - Ax1)T (Ax1 - b) and hence ⟨b - Ax1,A(x - x1)⟩ = 0. Thus,
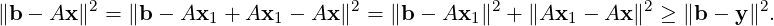
The above corollary gives the following result.
Proof. Part 1 directly follows from Corollary 5.3.5. For Part 2, let b = y + v, for y ∈ Col(A)
and v ∈ Null(AT ). As y ∈ Col(A), there exists x0 ∈ ℝn such that Ax0 = y. Thus, by
Remark 5.3.3, AT b = AT (y + v) = AT y = AT Ax0. Now, using the definition of pseudo-inverse (see
Exercise 1.3.7.14), we see that

 DRAFT
DRAFT
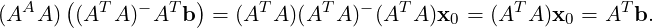
We now give a few examples to understand projections.
Example 5.3.6. Use the fundamental theorem of linear algebra to compute the vector of the orthogonal projection.
![([1,- 1,1,- 1,1])](LA1656x.png) .
. 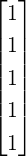 , where B =
, where B = 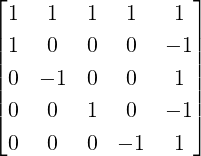 equals x =
equals x = 
 . Thus, the
projection is
. Thus, the
projection is 
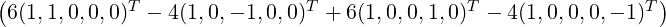 =
=
 (2,3,2,3,2)T .
(2,3,2,3,2)T .
![([1,1,- 1])](LA1664x.png) .
. 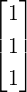 , where B =
, where B = 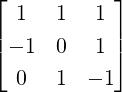 equals x =
equals x = 
 . Thus, the projection is
. Thus, the projection is

 =
=  (1,1,2)T .
(1,1,2)T .
![( T)
[1,2,1]](LA1672x.png) .
. 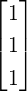 , where B =
, where B =  gives
gives  (1,2,1)T as the required vector.
(1,2,1)T as the required vector.
To use the first idea in Remark 5.3.3, we prove the following result which helps us to get the matrix of the orthogonal projection from an orthonormal basis.
Theorem 5.3.7. Let {f1,…,fk} be an orthonormal basis of a finite dimensional subspace W of an ips V. Then PW = ∑ i=1kfifi*.
Proof. Let v ∈ V. Then,
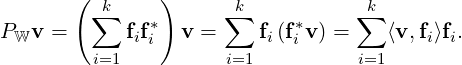
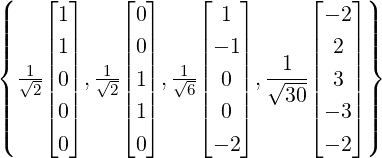
Example 5.3.8. In each of the following, determine the matrix of the orthogonal projection. Also, verify that PW + PW⊥ = I. What can you say about Rank(PW⊥) and Rank(PW)? Also, verify the orthogonal projection vectors obtained in Example 5.3.6.
![([1,- 1,1,- 1,1])](LA1679x.png) .
.  . Thus,
. Thus,

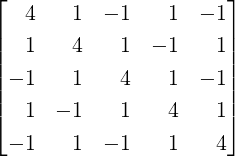 and
PW⊥ =
and
PW⊥ = 
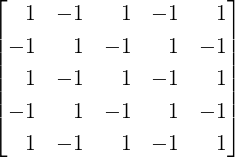 .
.
![([1,1,- 1])](LA1687x.png) .
. 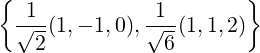 an
orthonormal basis of W. So,
an
orthonormal basis of W. So,
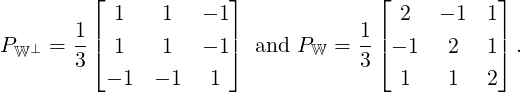
![([1,2,1]T )](LA1690x.png) ⊆ ℝ3.
⊆ ℝ3. 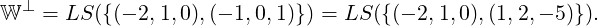
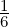
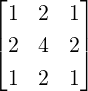 and P
W⊥ =
and P
W⊥ = 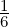
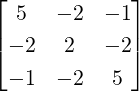 .
.

 DRAFT
DRAFT
We advise the readers to give a proof of the next result.
Theorem 5.3.9. Let {f1,…,fk} be an orthonormal basis of a subspace W of ℝn. If {f1,…,fn} is an extended orthonormal basis of ℝn, PW = ∑ i=1kfifiT and PW⊥ = ∑ i=k+1nfifiT then prove that
![[ ]
1 1
0 0](LA1698x.png) . Then, A is idempotent but not symmetric. Now, define P : ℝ2 → ℝ2 by
P(v) = Av, for all v ∈ ℝ2. Then,
. Then, A is idempotent but not symmetric. Now, define P : ℝ2 → ℝ2 by
P(v) = Av, for all v ∈ ℝ2. Then,
 W = [f1,…,fn-1].
Suppose
W = [f1,…,fn-1].
Suppose  = [f1,…,fn-1,fn] is an orthogonal ordered basis of ℝn obtained by extending
= [f1,…,fn-1,fn] is an orthogonal ordered basis of ℝn obtained by extending
 W. Now, define a function Q : ℝn → ℝn by Q(v) = ⟨v,fn⟩fn -∑
i=1n-1⟨v,fi⟩fi.
Then,
W. Now, define a function Q : ℝn → ℝn by Q(v) = ⟨v,fn⟩fn -∑
i=1n-1⟨v,fi⟩fi.
Then,
The function Q is called the reflection operator with respect to W⊥.
Theorem 5.3.9 implies that the matrix of the projection operator is symmetric. We use this idea to proceed further.
Definition 5.3.11. [Self-Adjoint Operator] Let V be an ips with inner product ⟨,⟩. A linear operator P : V → V is called self-adjoint if ⟨P(v),u⟩ = ⟨v,P(u)⟩, for every u,v ∈ V.
A careful understanding of the examples given below shows that self-adjoint operators and
Hermitian matrices are related. It also shows that the vector spaces ℂn and ℝn can be decomposed in
terms of the null space and column space of Hermitian matrices. They also follow directly from the
fundamental theorem of linear algebra.

 DRAFT
DRAFT
We now state and prove the main result related with orthogonal projection operators.
Theorem 5.3.13. Let V be a finite dimensional ips. If V = W ⊕ W⊥ then the orthogonal projectors
PW : V → V on W and PW⊥ : V → V on W⊥ satisfy

 DRAFT
DRAFT
Proof. Part 1: As V = W ⊕ W⊥, for each u ∈ W⊥, one uniquely writes u = 0 + u, where 0 ∈ W and u ∈ W⊥. Hence, by definition, PW(u) = 0 and PW⊥(u) = u. Thus, W⊥ ⊆ Null(PW) and W⊥⊆ Rng(PW⊥).
Now suppose that v ∈ Null(PW). So, PW(v) = 0. As V = W ⊕ W⊥, v = w + u, for unique w ∈ W and unique u ∈ W⊥. So, by definition, PW(v) = w. Thus, w = PW(v) = 0. That is, v = 0 + u = u ∈ W⊥. Thus, Null(PW) ⊆ W⊥.
A similar argument implies Rng(PW⊥) ⊆ W⊥ and thus completing the proof of the first part.
Part 2: Use an argument similar to the proof of Part 1.
Part 3, Part 4 and Part 5: Let v ∈ V. Then, v = w + u, for unique w ∈ W and unique u ∈ W⊥. Thus, by definition,
Hence, PW ∘ PW = PW, PW⊥∘ PW = 0V and IV = PW ⊕ PW⊥. Part 6: Let u = w1 + x1 and v = w2 + x2, for unique w1,w2 ∈ W and unique x1,x2 ∈ W⊥.
Then, by definition, ⟨wi,xj⟩ = 0 for 1 ≤ i,j ≤ 2. Thus,

 DRAFT
DRAFT
Remark 5.3.14. Theorem 5.3.13 gives us the following:
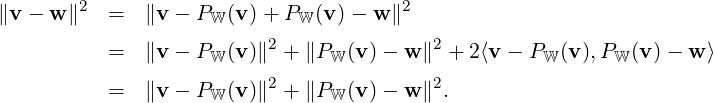

 DRAFT
DRAFT
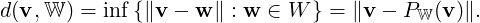
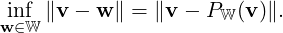
The next theorem is a generalization of Theorem 5.3.13. We omit the proof as the arguments are
similar and uses the following:
Let V be a finite dimensional ips with V = W1 ⊕ ⊕ Wk, for certain subspaces Wi’s of V. Then, for
each v ∈ V there exist unique vectors v1,…,vk such that
⊕ Wk, for certain subspaces Wi’s of V. Then, for
each v ∈ V there exist unique vectors v1,…,vk such that
 + vk.
+ vk.
Theorem 5.3.15. Let V be a finite dimensional ips with subspaces W1,…, Wk of V such that
V = W1 ⊕ ⊕ Wk. Then, for each i,j,1 ≤ i≠j ≤ k, there exist orthogonal projectors PWi : V → V of
V onto Wi satisfying the following:
⊕ Wk. Then, for each i,j,1 ≤ i≠j ≤ k, there exist orthogonal projectors PWi : V → V of
V onto Wi satisfying the following:
We now give the definition and a few properties of an orthogonal operator.
Definition 5.4.1. [Orthogonal Operator] Let V be a vector space. Then, a linear operator T : V → V is said to be an orthogonal operator if ∥T(x)∥ = ∥x∥, for all x ∈ V.
Example 5.4.2. Each T ∈ (V) given below is an orthogonal operator.
(V) given below is an orthogonal operator.
 ⟨x,a⟩a,x - ⟨x,a⟩a
⟨x,a⟩a,x - ⟨x,a⟩a = 0. Also, by
Pythagoras theorem ∥x -⟨x,a⟩a∥2 = ∥x∥2 - (⟨x,a⟩)2. Thus,
= 0. Also, by
Pythagoras theorem ∥x -⟨x,a⟩a∥2 = ∥x∥2 - (⟨x,a⟩)2. Thus,
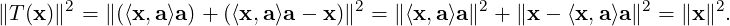

 DRAFT
DRAFT
![[ ]
cos θ - sinθ
sinθ cosθ](LA1726x.png)
![[ ]
x
y](LA1727x.png) .
.We now show that an operator is orthogonal if and only if it preserves the angle.
Proof. 1 ⇒2 Let T be an orthogonal operator. Then, ∥T(x + y)∥2 = ∥x + y∥2. So, ∥T(x)∥2 + ∥T(y)∥2 + 2⟨T(x),T(y)⟩ = ∥T(x) + T(y)∥2 = ∥T(x + y)∥2 = ∥x∥2 + ∥y∥2 + 2⟨x,y⟩. Thus, using definition again ⟨T(x),T(y)⟩ = ⟨x,y⟩.
2 ⇒1 If ⟨T(x),T(y)⟩ = ⟨x,y⟩, for all x,y ∈ V then T is an orthogonal operator as ∥T(x)∥2 = ⟨T(x),T(x)⟩ = ⟨x,x⟩ = ∥x∥2. _
As an immediate corollary, we obtain the following result.
Corollary 5.4.4. Let T ∈ (V). Then, T is an orthogonal operator if and only if “for every
orthonormal basis {u1,…,un} of V, {T(u1),…,T(un)} is an orthonormal basis of V”. Thus, if
(V). Then, T is an orthogonal operator if and only if “for every
orthonormal basis {u1,…,un} of V, {T(u1),…,T(un)} is an orthonormal basis of V”. Thus, if
 is an orthonormal ordered basis of V then T
is an orthonormal ordered basis of V then T![[B,B]](LA1730x.png) is an orthogonal matrix.
is an orthogonal matrix.
Definition 5.4.5. [Isometry, Rigid Motion] Let V be a vector space. Then, a map T : V → V
is said to be an isometry or a rigid motion if ∥T(x) - T(y)∥ = ∥x - y∥, for all x,y ∈ V.
That is, an isometry is distance preserving.

 DRAFT
DRAFT
Observe that if T and S are two rigid motions then ST is also a rigid motion. Furthermore, it is clear from the definition that every rigid motion is invertible.
We now prove that every rigid motion that fixes origin is an orthogonal operator.
Theorem 5.4.7. Let V be a real ips. Then, the following statements are equivalent for any map T : V → V.

 DRAFT
DRAFT
Proof. We have already seen the equivalence of Part 2 and Part 3 in Theorem 5.4.3. Let us now prove the equivalence of Part 1 and Part 2/Part 3.
If T is an orthogonal operator then T(0) = 0 and ∥T(x) - T(y)∥ = ∥T(x - y)∥ = ∥x - y∥. This proves Part 3 implies Part 1.
We now prove Part 1 implies Part 2. So, let T be a rigid motion that fixes 0. Thus, T(0) = 0 and ∥T(x) -T(y)∥ = ∥x - y∥, for all x,y ∈ V. Hence, in particular for y = 0, we have ∥T(x)∥ = ∥x∥, for all x ∈ V. So,
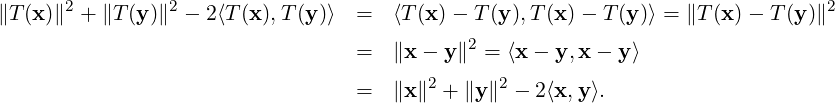
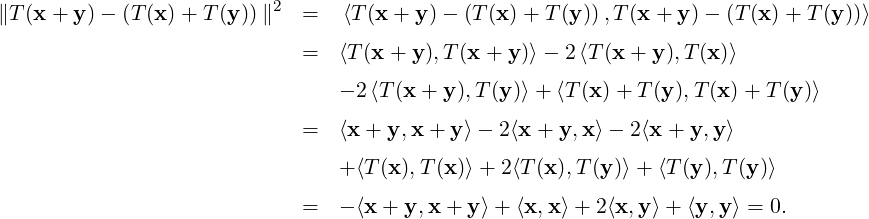
Thus, T(x + y) -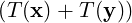 = 0 and hence T(x + y) = T(x) + T(y). A similar calculation
gives T(αx) = αT(x) and hence T is linear. _
= 0 and hence T(x + y) = T(x) + T(y). A similar calculation
gives T(αx) = αT(x) and hence T is linear. _

 DRAFT
DRAFT
Prove that Orthogonal and Unitary congruences are equivalence relations on Mn(ℝ) and Mn(ℂ), respectively.
![xeiθ = (x1 + ix2)(cosθ + isinθ ) = x1 cosθ - x2 sin θ + i[x1sinθ + x2cosθ].](LA1741x.png)
![[ ] [ ][ ]
x1 cosθ - x2 sin θ = cosθ - sinθ x1 .
x1 sin θ + x2 cosθ sinθ cosθ x2](LA1742x.png)
![[ ]
cosθ - sinθ
sinθ cosθ](LA1743x.png) , the matrix of the corresponding rotation? Justify.
, the matrix of the corresponding rotation? Justify.

 DRAFT
DRAFT
![[ ]
cosθ sinθ
- sinθ cosθ](LA1744x.png) , for θ ∈ ℝ. Then, A is an orthogonal matrix if and
only if A = T(θ) or A =
, for θ ∈ ℝ. Then, A is an orthogonal matrix if and
only if A = T(θ) or A = ![[ ]
0 1
1 0](LA1745x.png) T(θ), for some θ ∈ ℝ.
T(θ), for some θ ∈ ℝ.

 DRAFT
DRAFT
![∥x ∥1 = max {|xi| : xT = [x1,...,xn]}.](LA1750x.png)
In the previous chapter, we learnt that if V is vector space over F with dim(V) = n then V basically looks like Fn. Also, any subspace of Fn is either Col(A) or Null(A) or both, for some matrix A with entries from F.
So, we started this chapter with inner product, a generalization of the dot product in ℝ3 or ℝn. We
used the inner product to define the length/norm of a vector. The norm has the property that “the
norm of a vector is zero if and only if the vector itself is the zero vector”. We then proved the
Cauchy-Bunyakovskii-Schwartz Inequality which helped us in defining the angle between two

 DRAFT
vector. Thus, one can talk of geometrical problems in ℝn and proved some geometrical
results.
DRAFT
vector. Thus, one can talk of geometrical problems in ℝn and proved some geometrical
results.
We then independently defined the notion of a norm in ℝn and showed that a norm is induced by an inner product if and only if the norm satisfies the parallelogram law (sum of squares of the diagonal equals twice the sum of square of the two non-parallel sides).
The next subsection dealt with the fundamental theorem of linear algebra where we showed that if A ∈ Mm,n(ℂ) then
 Col(A*)
Col(A*)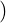 ⊥ and Null(A*) =
⊥ and Null(A*) =  Col(A)
Col(A)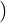 ⊥.
⊥.
We then saw that having an orthonormal basis is an asset as determining the
So, the question arises, how do we compute an orthonormal basis? This is where we came across the Gram-Schmidt Orthonormalization process. This algorithm helps us to determine an orthonormal basis of LS(S) for any finite subset S of a vector space. This also lead to the QR-decomposition of a matrix.
Thus, we observe the following about the linear system Ax = b. If
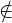 Col(A) then in most cases we need a vector x such that the least square error between
b and Ax is minimum. We saw that this minimum is attained by the projection of b on
Col(A). Also, this vector can be obtained either using the fundamental theorem of linear
algebra or by computing the matrix B(BT B)-1BT , where the columns of B are either the
pivot columns of A or a basis of Col(A).
Col(A) then in most cases we need a vector x such that the least square error between
b and Ax is minimum. We saw that this minimum is attained by the projection of b on
Col(A). Also, this vector can be obtained either using the fundamental theorem of linear
algebra or by computing the matrix B(BT B)-1BT , where the columns of B are either the
pivot columns of A or a basis of Col(A).
 DRAFT
DRAFT

 DRAFT
DRAFT