Use of mathematical model to understand flame characteristics under certain controlled conditions. It mimics a real-life situation.

Elements of mathematical model:


• Equations (also called governing equations) that describe behavior of the system under consideration.


• Auxiliary equations (also called boundary conditions) that describe how the system can be modified.


• Methods and algorithms to combine the above two elements in order to obtain numeric data for a given set of conditions.

Importance of laminar premixed flame:


• Simplest of the flame configurations


• Essential for understanding of practical combustion systems


• Model problem for combustion

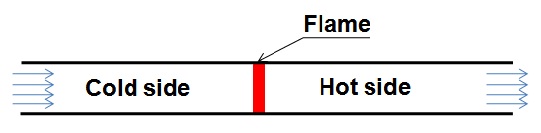
Typical configuration:




• Flame is situated in a flowing mixture of methane fuel and atmospheric air.


• Far away from the flame to the left, no reaction occurs -> cold boundary.


• Reactions and heat release occurs in a narrow region.


• To the right, only products exist at high temperatures.

Problem Definition


• Model the behavior of flame in response to changes in equivalence ratio.


• Describe flame structure; calculate burning velocity at three equivalence ratios.

• During the combustion process:
  • The components and heat are transported from flame zone to other locations.
  • Mass diffusion and heat conduction occur predominantly near the flame.


• Governing equations should reflect these physical processes in terms of
  • Physical laws of motion (Newton's laws)
  • Energy (first law of thermodynamics)
  • Mass conservation


• Our task:
  • Apply these principles to a reacting flow process.
  • Take into account the simplifying assumptions.
  • Build a model of the laminar premixed flame.